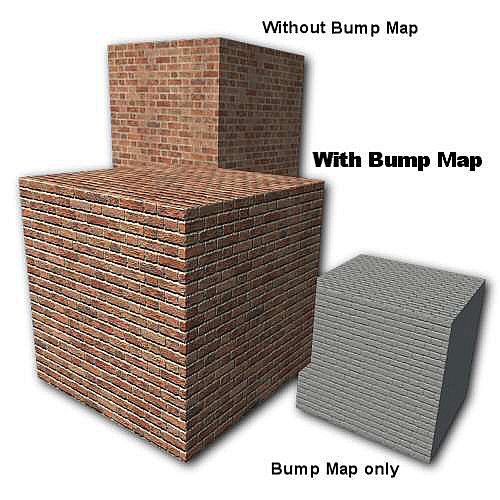
Bump Mapping
← 2D Billboards | ● | 2D Displacement Mapping →
Beobachtung: Oberflächen haben kleine Dellen und Erhebungen. Diese verändern die Normale der Oberfläche und damit die Beleuchtung.
Idee: Benutze Textur um die Normale einer planaren Oberfläche zu verändern.
Schritt 1) Height Mapping:
Grau Kanal der Textur wird als Höhenveränderung interpretiert, d.h. Bump Map = Greyscale Height Map
Aus der Höhenveränderung werden die Normalen extrahiert und in einer Normal Map gespeichert.
Schritt 2) Normal Mapping:
RGB Kanäle der Textur werden als die 3 Komponenten XYZ der Normale in Objektkoordinaten interpretiert:
Mit diesen Texturwerten werden die Normalen der planaren Oberfläche im Tangentenraum (Tangent Space, repräsentiert über die Matrix TBN, variiert und anschlieÃend die Beleuchtungsberechnung durchgeführt (Blinn-Phong).
 wikimedia
wikimediaDer Tangentenraum wird aufgespannt durch die drei Vektoren Tangente, Bitangente und Normale des Raums. Die Normale ist durch die Geometrie gegeben (unabhängig von den Normalen in der Normal Map), die beiden Tangenten kann man frei wählen.
Damit der aufgespannte Raum zur Normal Map passt, müssen die beiden Tangenten der x- und y-Richtung der Textur entsprechen. Dazu muss im üblichen Ansatz zumindest die Tangente als weiteres Attribut im Hauptprogramm per Vertex aus Koordinaten und Texturkoordinaten berechnet und den Vertex Shader übergeben werden. Die Bitangente bekommt man über Kreuzprodukt der Tangente und der Normalen.
Der oft erwähnte Ansatz, die Beleuchtungsberechnung im Tangentenraum selber durchzuführen und dafür die Lichtrichtung und den View-Vektor in den Tangentenraum zu transferieren (über die inverse TBN), dient nur der Beschleunigung (mehr Berechnung im Vertex-Shader, weniger im Fragment-Shader).
Eine der erfolgreichsten Varianten vorgestellt durch Christian Schüler in der ShaderX Buchreihe ist die Nutzung der Normal Map ohne Tangentenvektor, indem der Tangent Space direkt aus partiellen Ableitungen der Texturkoordinaten und des View-Vektors berechnet wird - was in GLSL sehr einfach möglich ist.
Die dahinter stehende Mathematik ist ziemlich involviert, aber nachvollziehbar, der Shader dafür recht kompakt und quasi trivial nutzbar.
Achtung:
Manche Tutorials wie - nur beispielhaft - opengl-tutorial.org sind zwar ausführlich und einleuchtend, aber auch manchmal falsch und verwirrend (hier: TBN ist eigentlich die inverse TBN). Und fast alle Tutorials nutzen den Tangent Space, auch wenn eigentlich der Cotangent Space genutzt werden müsste. Ist der Tangentenraum orthonomal, ist die Unterscheidung aber nicht relevant. Mehr dazu in der ausführlichen Darstellung von Christian Schüler (beware, here be mathematical dragons).
← 2D Billboards | ● | 2D Displacement Mapping →