Signed Distance Functions
← Raymarching | ● | Raymarching mit OpenGL →
Eine andere häufig genutzte Variante nutzt Signed Distance Functions (SDF) zur Bestimmung der Abtastrate.
Eine Signed Distance Function ermittelt fĂĽr die bekannte Geometrie den Abstand eines Samplepunktes zur Geometrie. Im inneren der Geometrie ist diese negativ. Die SDF der gesamten Geometrie ist gleich dem Minimum aller SDF in der Szene.
Beispiel: SDF einer Kugel an der Position $\vec c$ mit Radius $r$:
Weitere SDFs zu verschiedenen Primitiven hat Inigo Quilez (iq) gesammelt. Mit Hilfe von SDFs kann auch einfach Constructive Solid Geometry (CSG) implementiert werden.
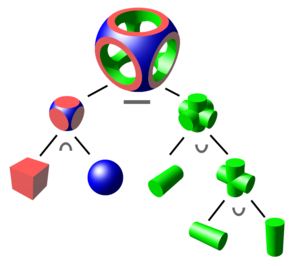
CC BY-SA 3.0 Wikimedia User:Zottie
Wie man mit SDFs auch komplexe Geometrien darstellen kann, zeigt ein beeindruckendes Demo von iq deutlich. Die zugrundeliegenden Ăśberlegungen gibt es in einem YouTube Video.
Sphere Tracing
Mit der SDF der Szene als Abtastrate ist man sicher, dass man keine Geometrie übersieht, und Leerräume können sehr schnell durchschritten werden. Dafür trifft man i.d.R. nie exakt die Geometrie, man muss also beim Unterschreiten eines Epsilons einen Treffer annehmen.
Dieses Verfahren nennt man Sphere-Tracing, da in jedem Schritt die Schrittweite von der Größe der Kugel abhängt, in der keine Geometrie zu finden ist. Hier eine interaktive Demo auf shadertoy.
Die ganzen Verfahren können auch kombiniert werden. Die Komplexität steigt entsprechend.
← Raymarching | ● | Raymarching mit OpenGL →