GL Tesselierungsbeispiel
← GL Tesselierung | ● | 2D Textur Mapping →
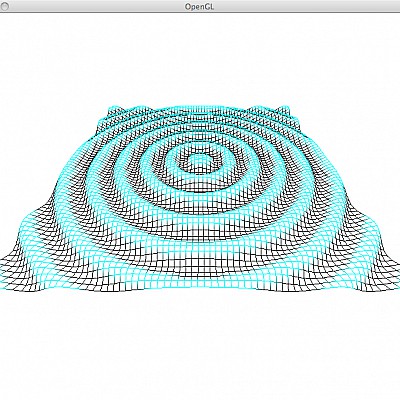
Tesselierung der Funktion
durch regelmĂ€Ăiges Gitter aus Quads (Quadmesh):
{return(3*sin(sqrt(x*x+y*y)/3));}
glBegin(GL_QUADS);
for (i=-100; i<=100-step; i+=step)
for (j=-100; j<=100-step; j+=step)
{
float f0=func(i,j);
glColor3f(0,f0,f0);
glVertex3d(i,j,f0);
float f1=func(i+step,j);
glColor3f(0,f1,f1);
glVertex3d(i+step,j,f1);
float f2=func(i+step,j+step);
glColor3f(0,f2,f2);
glVertex3d(i+step,j+step,f2);
float f3=func(i,j+step);
glColor3f(0,f3,f3);
glVertex3d(i,j+step,f3);
}
glEnd();
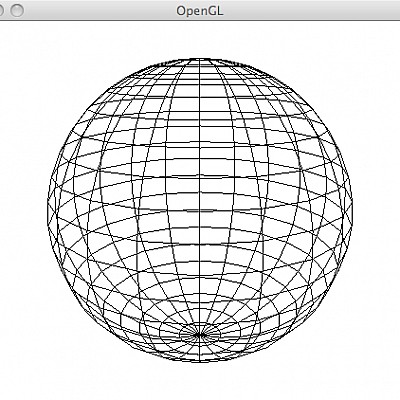
Tesselierung einer Kugel in Polarkoordinaten:
Kugelkoordinaten:
{
glBegin(GL_QUAD_STRIP);
for (i=0; i<=200; i+=step)
{
alpha=(float)i/100*M_PI;
beta1=(float)j/100*M_PI/2;
beta2=(float)(j+step)/100*M_PI/2;
glVertex3d(sin(alpha)*sin(beta1),
cos(beta1),
cos(alpha)*sin(beta1));
glVertex3d(sin(alpha)*sin(beta2),
cos(beta2),
cos(alpha)*sin(beta2));
}
glEnd();
}
Anwendungsbeispiele aus Blender 2.8 (Alpha)
Die Beispiele oben finden auch eine reale Anwendung in Blender. Grundobjekte lassen sich mathematisch beschreiben und so sehr einfach in unterschiedlichen Detailstufen generieren. Am Beispiel der Kugel funktioniert das wie folgt:
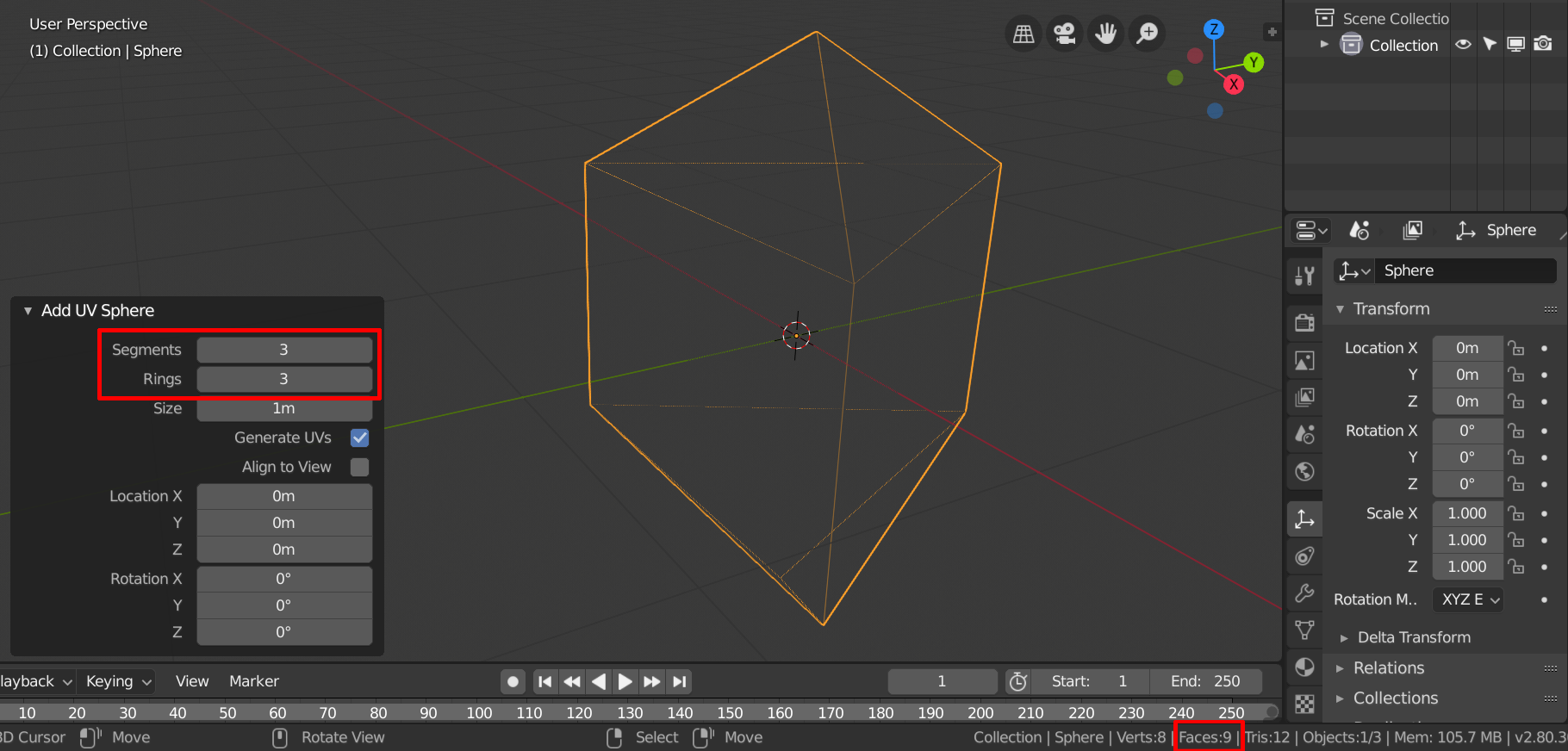
Niedrig aufgelöste Kugel
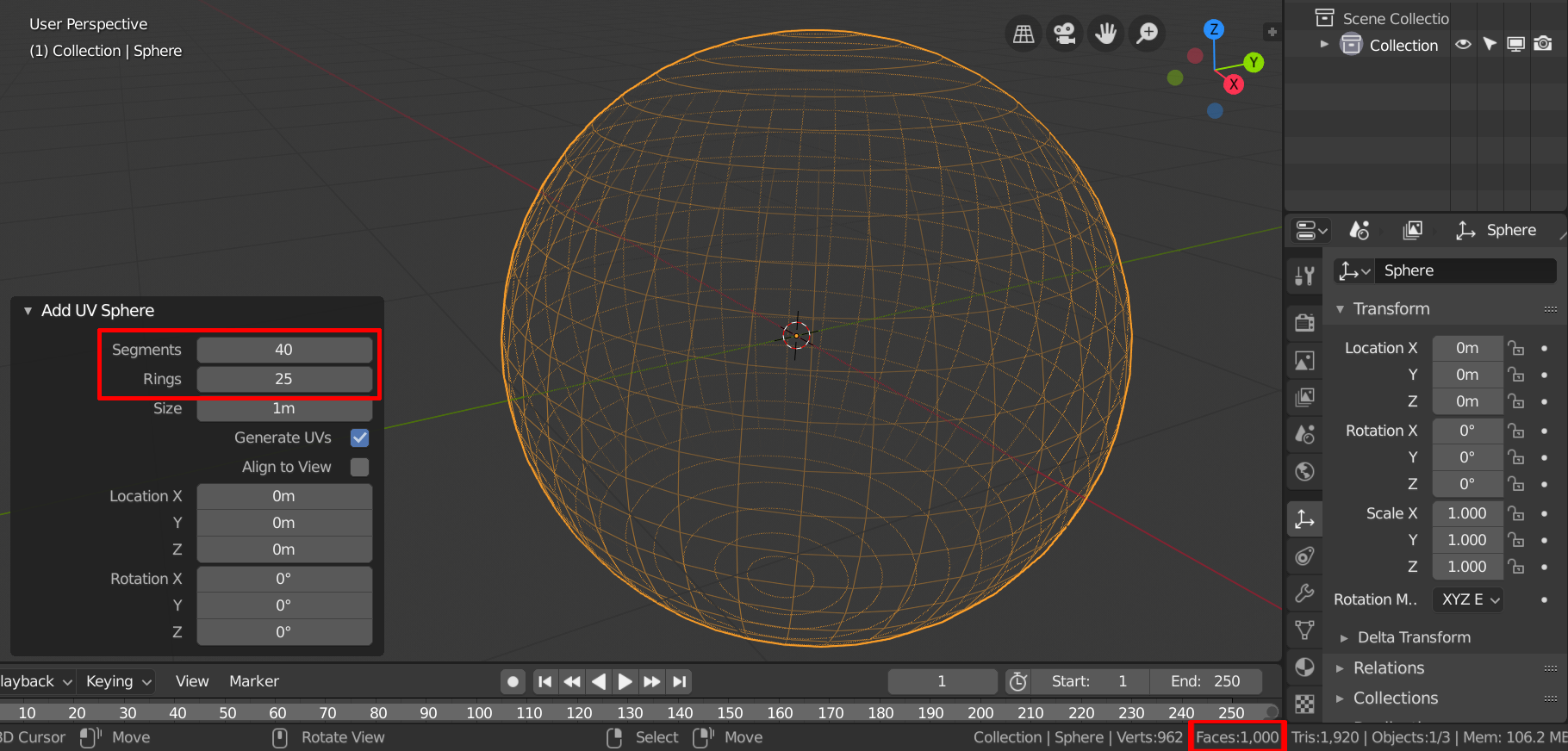
Hoch aufgelöste Kugel
Die Gesamtzahl der Polygone lÀsst sich beispielsweise sehr einfach mit $ \text{faces}=\text{segments} \cdot \text{rings} $ berechnen.
Es ist ebenfalls möglich neue Objekte durch die Angabe von mathematischen Funktionen zu generieren. Dazu muss jedoch zunĂ€chst ein Addon in Blender aktiviert werden (vgl. altes Tutorial zu 3D Function Surfaces). Ein Beispiel fĂŒr die prozedurale Generierung des Meshes fĂŒr einen verdrehten Torus ist nachfolgend zu sehen:
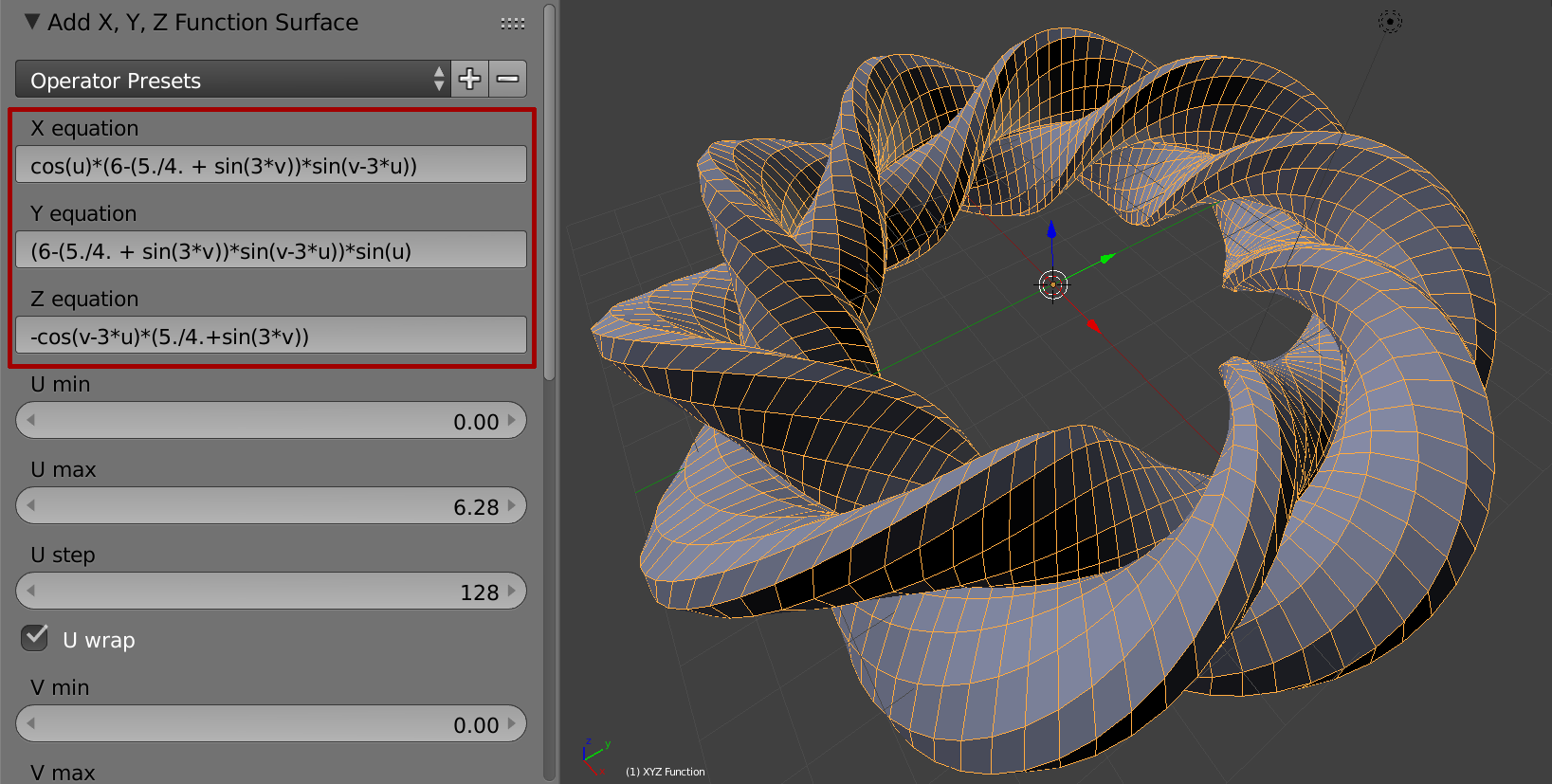
3D Function Surfaces (alte Blenderversion)
Etwas komplizierter sieht es aus, wenn man ein beliebiges Objekt tesselieren möchte. Dazu verwendet man in der Regel den Subdivision Surface Modifier, welcher entweder im Modus Simple jedes vierseitige Polygon (Quad) in vier weitere Polygone aufteilt oder im Modus Catmull-Clark zusÀtzlich das Objekt nach jeder Tesselierungsstufe abrundet. Nachfolgend an Blenders Maskottchen Suzanne demonstriert:
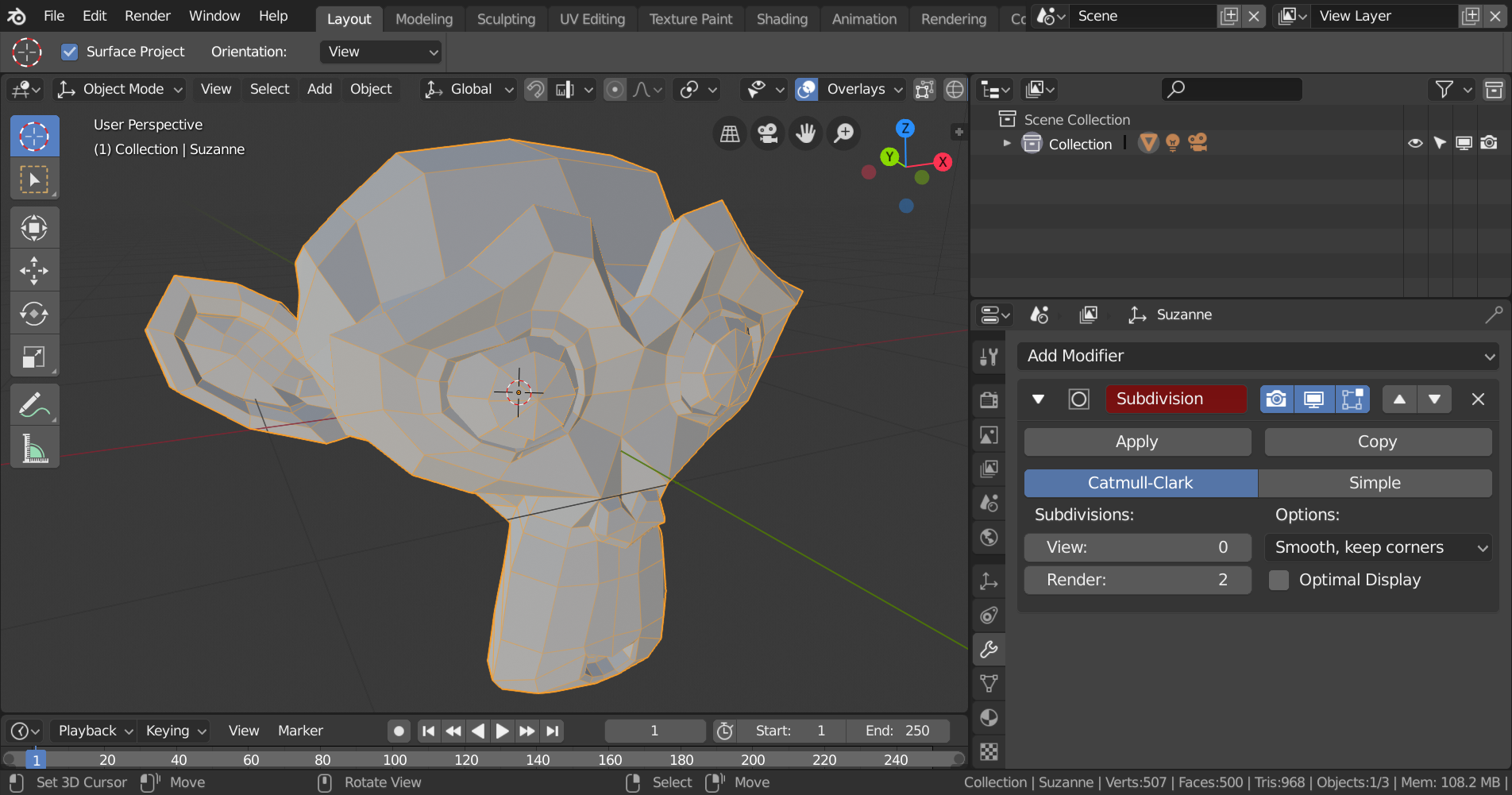
Suzanne ohne Tesselierung
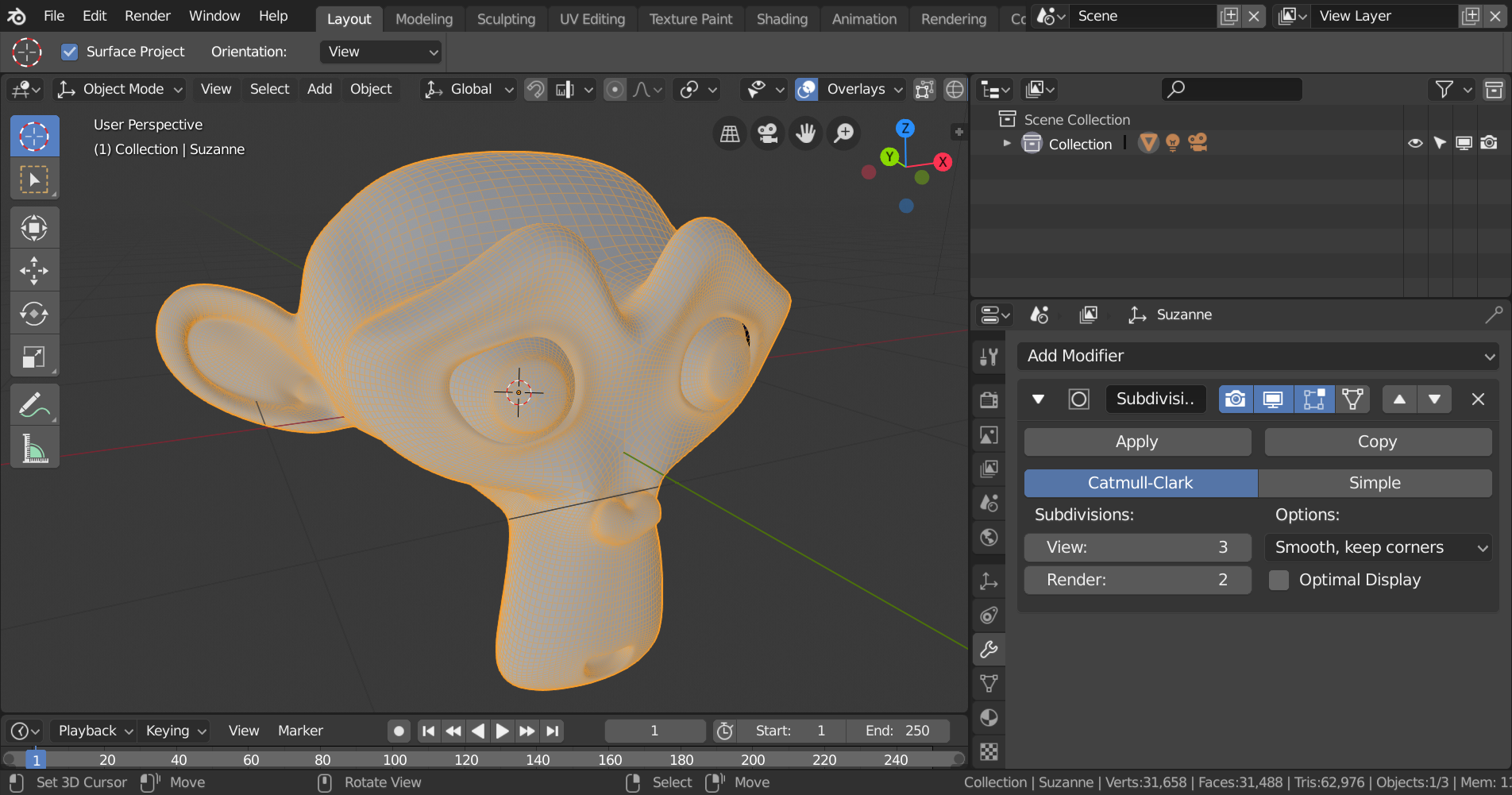
Suzanne mit dreifacher Catmull-Clark-Tesselierung
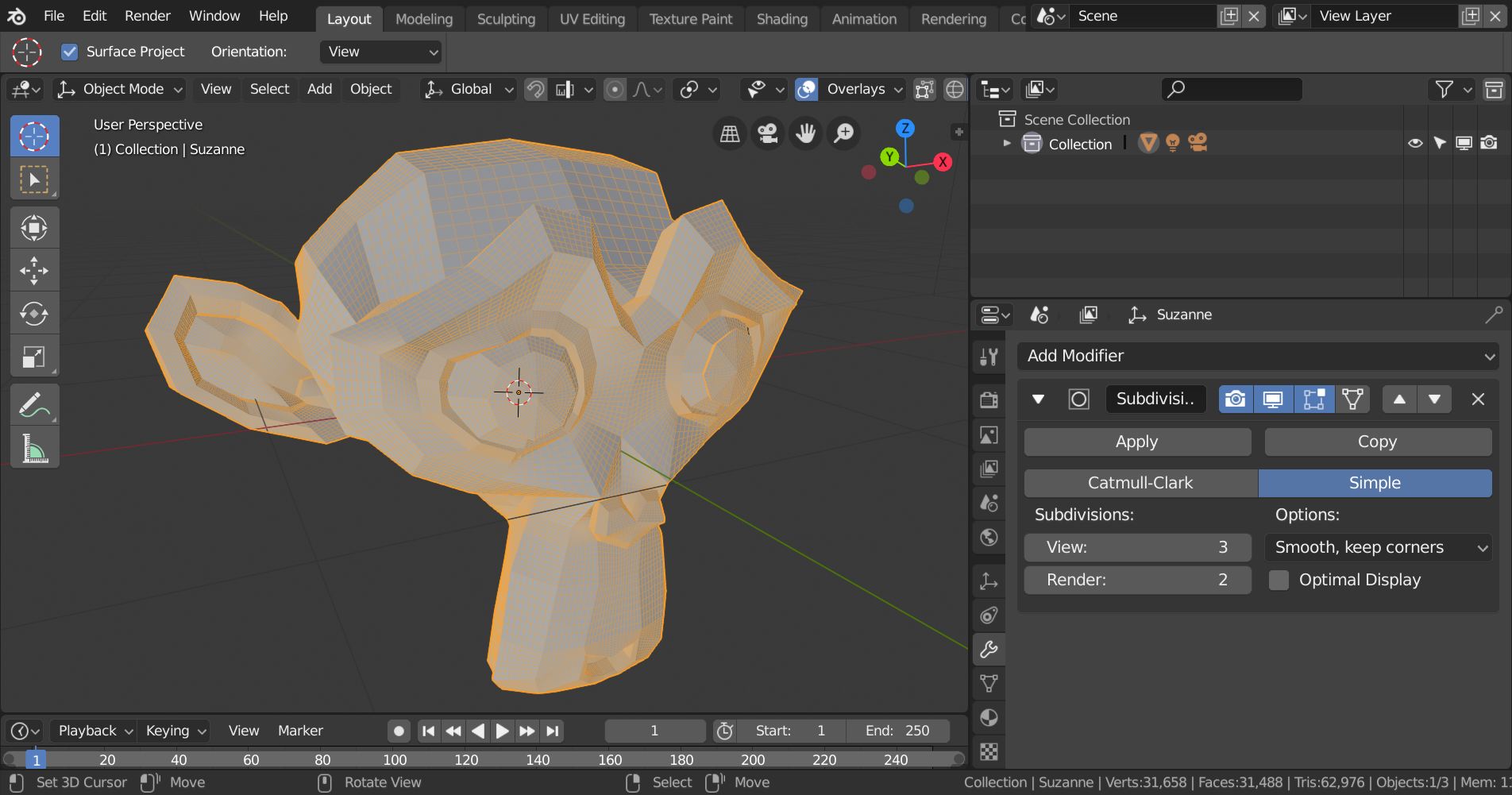
Suzanne mit dreifacher Simple-Tesselierung
Die Berechnung der Gesamtzahl der Polygone im Falle von Quadmeshes (vier Punkte pro Polygon) ist nur minimal komplizierter als die fĂŒr mathematische OberflĂ€chen und lĂ€sst sich mit $ \text{subdivided_faces}=\text{faces} \cdot 4^{\text{subdivisions}} $ berechnen. Die Umkehrung von Tesselierung wird meist als Dezimierung (Decimation) oder Remeshing bezeichnet. Man verwendet es beispielsweise zur Realisierung von Level-Of-Detail (LOD, Beispiel in Blender). Bei diesen Verfahren wird abhĂ€ngig von der Kameradistanz das Objekt entweder detailliert (geringe Distanz) oder stark vereinfacht (groĂe Distanz) dargestellt.
Bisher haben wir nur die gleichmĂ€Ăige Tesselierung anhand von einigen Beispielen betrachtet. Manchmal kann es jedoch sinnvoll sein, die Tesselierung nur in bestimmten Bereichen eines Objekts zu erhöhen, z.B. dort wo mehr Details gewĂŒnscht sind. Beim digitalen Bildhauen (Sculpting) gibt es in Blender die Möglichkeit Dynamic Topology zu aktivieren und so wĂ€hrend der Bearbeitung das Mesh mit bestimmten Pinseln adaptiv zu tesselieren:
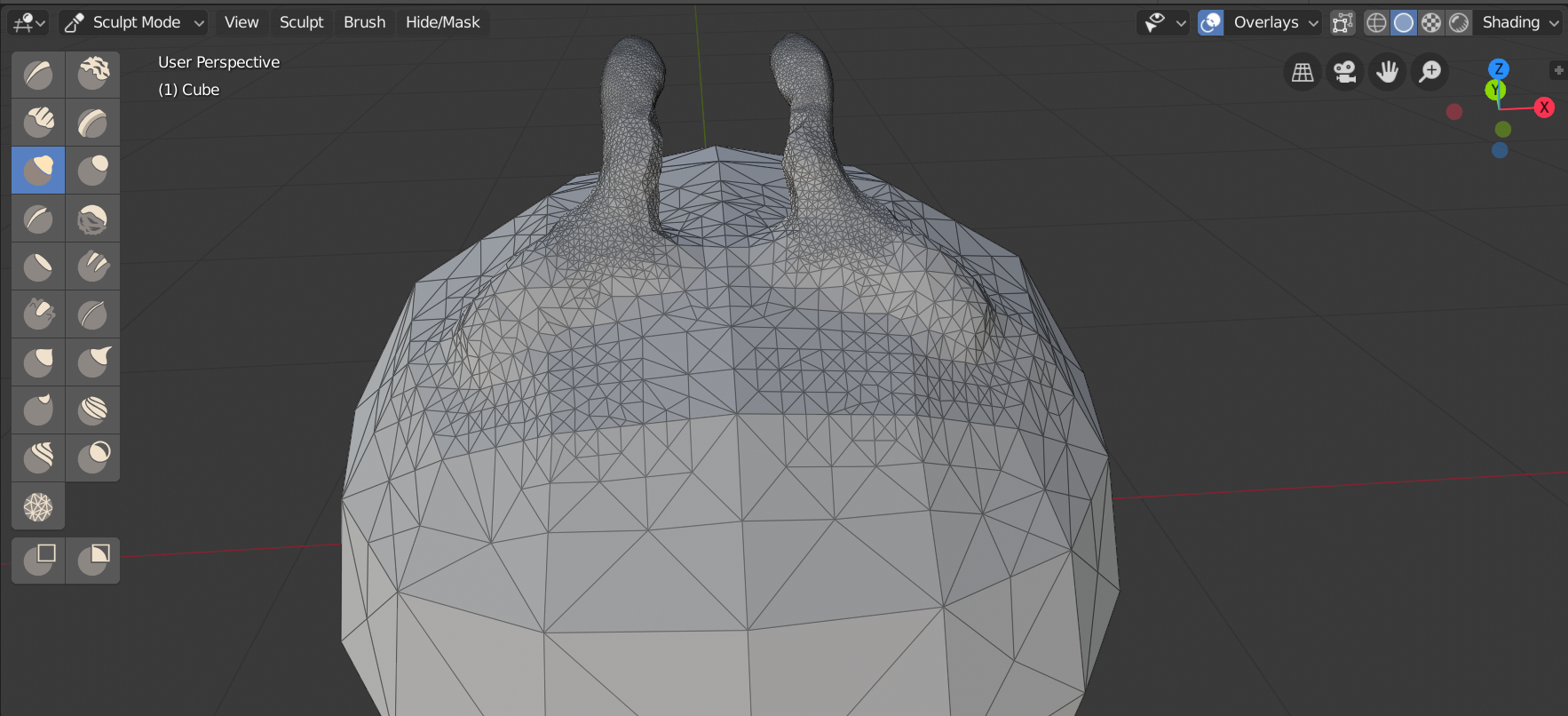
Sculpting in Blender mit Dynamic Topology
Besonders nĂŒtzlich ist das Konzept der Spline-basierten Modellierung, z.B. mit BĂ©zier Splines. Ein Kontrollpolygon definiert dabei eine Kurve im Raum. Diese Kurve lĂ€sst sich relativ einfach verĂ€ndern, indem nur die einzelnen Punkte des Kontrollpolygons verĂ€ndert werden. Die Konstruktion der BĂ©zier Spline auf Basis des Kontrollpolygons kann sehr leicht mithilfe des De Casteljau-Algorithmus veranschaulicht werden.
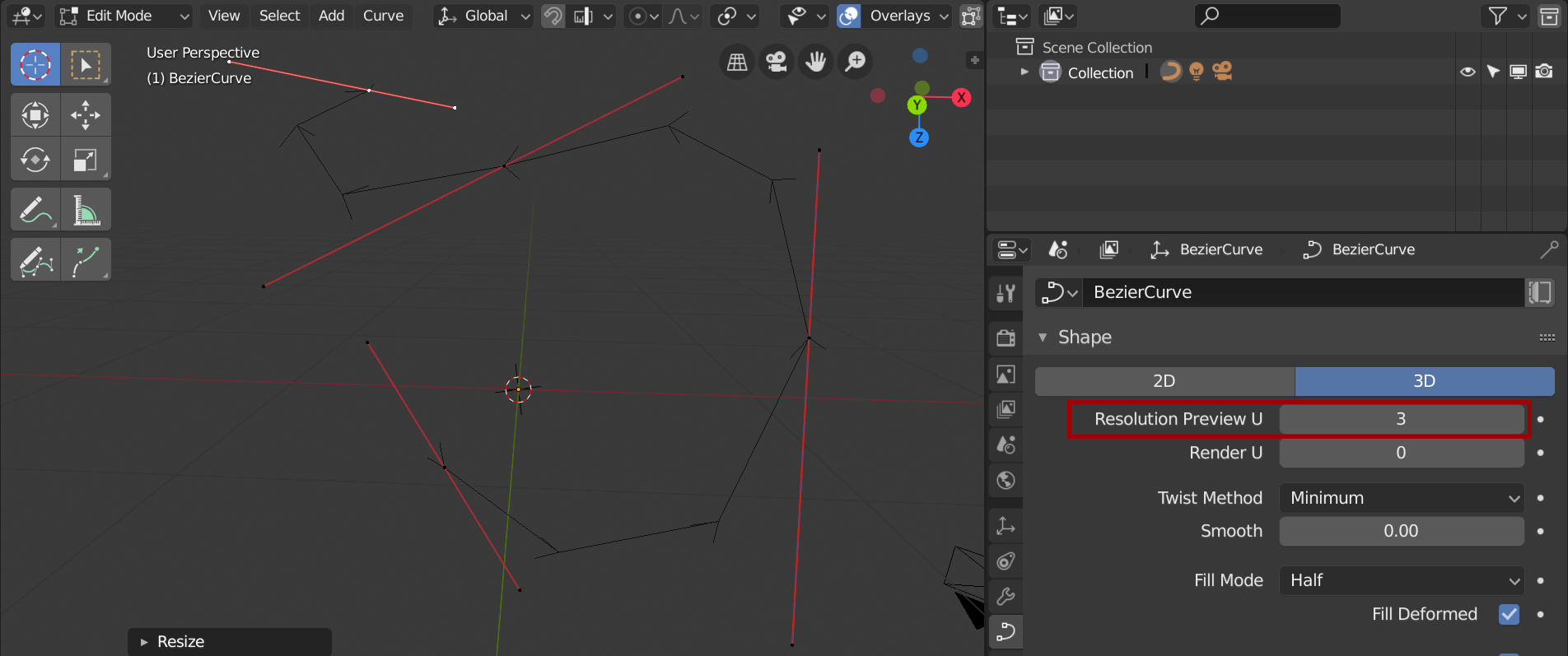
Wenig tesselierte BĂ©zierkurve
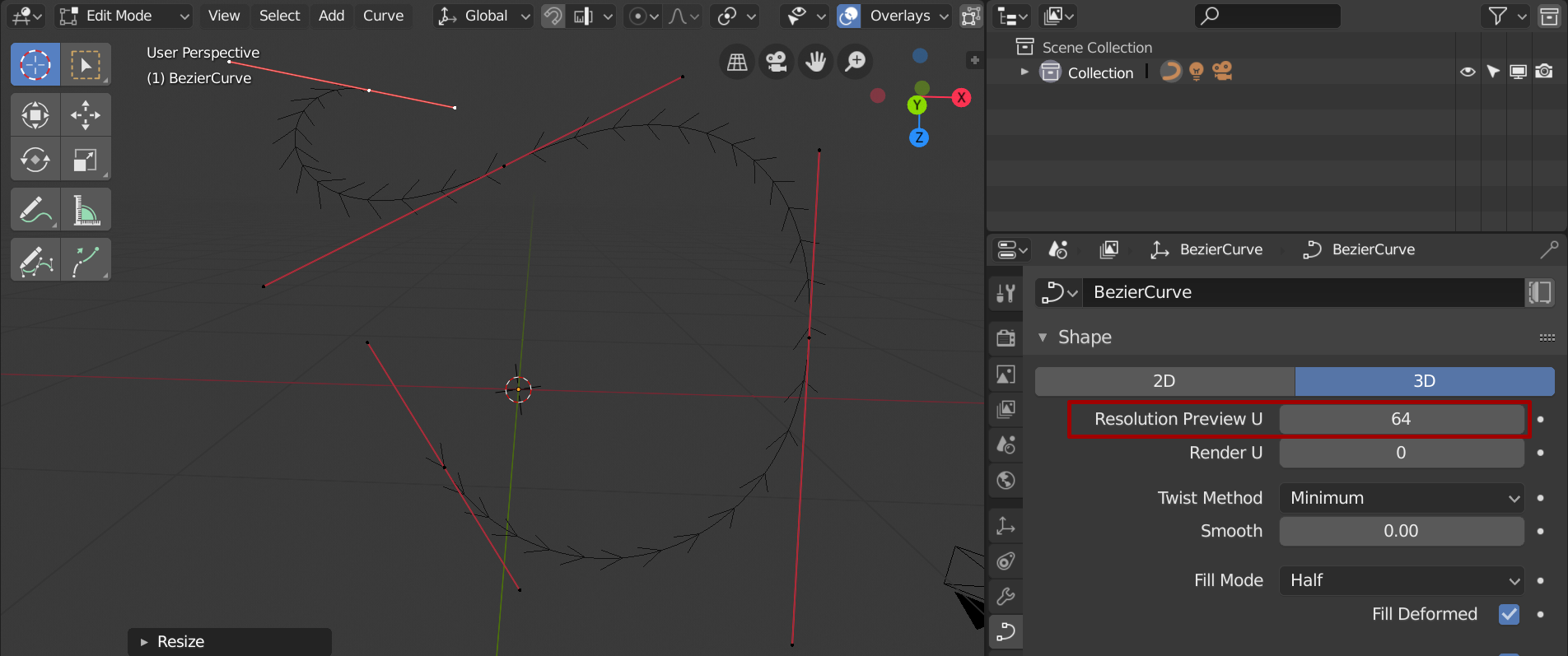
Stark tesselierte BĂ©zierkurve
Um mit Splines eine OberflÀche zu erzeugen, gibt es verschiedene Methoden. Einerseits kann entlang dieser Spline neue Geometrie extrudiert werden. Andererseits können OberflÀchen durch mehrere Splines beschrieben werden und so Bézier-Surfaces formen. Diese Splines bilden dann ein Kontrollgitter, wie nachfolgend dargestellt.
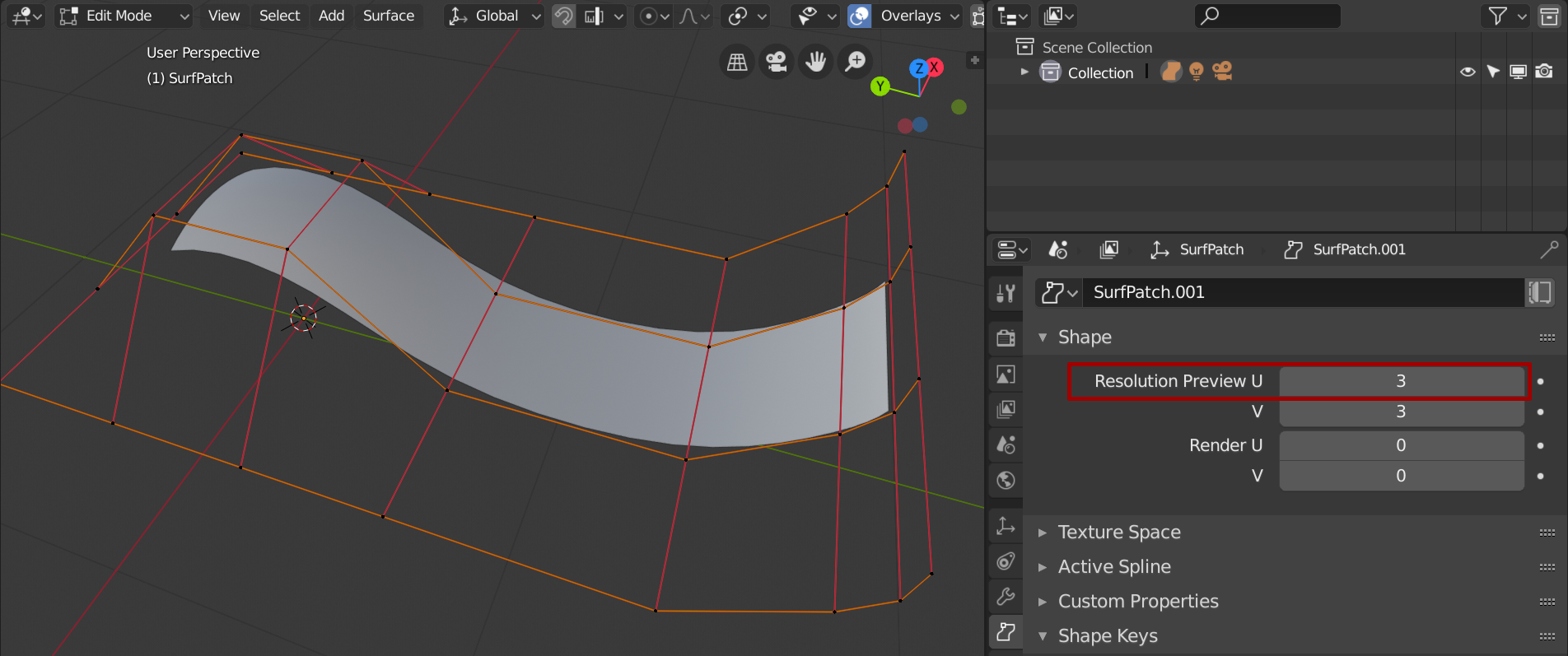
Non-Uniform Rational B-Spline (NURBS) Surface in Blender
Eine besonders gute ErklĂ€rung zur prozeduralen Erzeugung von Dreiecksnetzen mithilfe von Splines aus dem Gebiet der Spieleentwicklung gab es auf der Konferenz Unite 2015 mit dem Titel “A coder’s guide to spline-based procedural geometry”.
← GL Tesselierung | ● | 2D Textur Mapping →