Computergrafik

Algorithmus von De Casteljau

← Bezier Curves | ● | Bezier Patches →

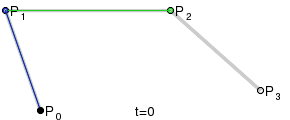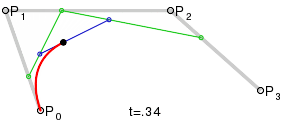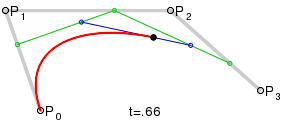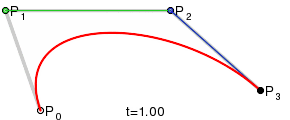
Konstruktion des BezierPunktes B=F(t):

  • Mit dem Parameter t die Strecken, definiert durch die n Kontrollpunkte, im Verhältnis t:1-t teilen.
  • Die so erzeugten Punkte ergeben eine neue Serie von n-1 Kontrollpunkten.
  • Solange wiederholen bis ein Punkt übrig bleibt.
wikipedia.org

Siehe auch wikipedia.

Rekurrenz für kubische Bezierkurven:

Die Punkte $P_0, Q_0, R_0, B$ und die Punkte $B, R_1, Q_2, P_3$ sind die Kontrollpunkte für zwei neue kubische Bezierkurven

Rekursiver Zeichenalgorithmus: 

drawcurve(p0,p1,p2,p3)
{
   if (|p0-p3|<eps) drawline(p0,p3);
   else
   {
      q0=(p0+p1)/2;
      q1=(p1+p2)/2;
      q2=(p2+p3)/2;

      r0=(q0+q1)/2;
      r1=(q1+q2)/2;

      b=(r0+r1)/2;

      drawcurve(p0,q0,r0,b);
      drawcurve(b,r1,q2,p3);
   }
}

Q Kann man mit kubischen Bezierkurven ein Kreissegment darstellen?

Nein, dazu benötigt man rationale Bezierkurven. Siehe dazu eine grafische Erklärung auf StackOverflow.

← Bezier Curves | ● | Bezier Patches →

Options: