VolumeRendering
Case Table in C++
← Slicing Case Table | ● | Maximum Intensity Projection →
Decomposition cases as C++ switch:
#include "v3d.h"
// extract 1 triangle from a tetrahedron
// v0 is the cutaway vertex
// d is distance of the respective point to the cutting plane
void slice1tri(const v3d &v0,const double d0,
const v3d &v1,const double d1,
const v3d &v2,const double d2,
const v3d &v3,const double d3)
{
v3d p0,p1,p2;
p0=(d1*v0+d0*v1)/(d0+d1);
p1=(d2*v0+d0*v2)/(d0+d2);
p2=(d3*v0+d0*v3)/(d0+d3);
glBegin(GL_TRIANGLES);
glTexCoord3d(p0.x,p0.y,p0.z);
glVertex3d(p0.x,p0.y,p0.z);
glTexCoord3d(p1.x,p1.y,p1.z);
glVertex3d(p1.x,p1.y,p1.z);
glTexCoord3d(p2.x,p2.y,p2.z);
glVertex3d(p2.x,p2.y,p2.z);
glEnd();
}
// extract 2 triangles (a quad) from a tetrahedron
// v0 is the start point of the cutaway line segment
// v1 is the end point of the cutaway line segment
// d is distance of the respective point to the cutting plane
void slice2tri(const v3d &v0,const double d0,
const v3d &v1,const double d1,
const v3d &v2,const double d2,
const v3d &v3,const double d3)
{
v3d p0,p1,p2,p3;
p0=(d2*v0+d0*v2)/(d0+d2);
p1=(d2*v1+d1*v2)/(d1+d2);
p2=(d3*v0+d0*v3)/(d0+d3);
p3=(d3*v1+d1*v3)/(d1+d3);
glBegin(GL_QUADS);
glTexCoord3d(p0.x,p0.y,p0.z);
glVertex3d(p0.x,p0.y,p0.z);
glTexCoord3d(p1.x,p1.y,p1.z);
glVertex3d(p1.x,p1.y,p1.z);
glTexCoord3d(p3.x,p3.y,p3.z);
glVertex3d(p3.x,p3.y,p3.z);
glTexCoord3d(p2.x,p2.y,p2.z);
glVertex3d(p2.x,p2.y,p2.z);
glEnd();
}
// extract a slice from a tetrahedron
// 2 cases: slice geometry consists of either 1 or 2 triangles
void slice(const v3d &v0, // vertex v0
const v3d &v1, // vertex v1
const v3d &v2, // vertex v2
const v3d &v3, // vertex v3
const v3d &o, // origin of cutting plane
const v3d &n) // normal of cutting plane
{
double d0,d1,d2,d3;
int ff;
d0=(v0-o)*n;
d1=(v1-o)*n;
d2=(v2-o)*n;
d3=(v3-o)*n;
ff=0;
if (d0<0.0) ff|=1;
if (d1<0.0) ff|=2;
if (d2<0.0) ff|=4;
if (d3<0.0) ff|=8;
switch (ff)
{
// 1 triangle
case 1: case 14: slice1tri(v0,fabs(d0),
v1,fabs(d1),
v2,fabs(d2),
v3,fabs(d3)); break;
case 2: case 13: slice1tri(v1,fabs(d1),
v0,fabs(d0),
v2,fabs(d2),
v3,fabs(d3)); break;
case 4: case 11: slice1tri(v2,fabs(d2),
v0,fabs(d0),
v1,fabs(d1),
v3,fabs(d3)); break;
case 8: case 7: slice1tri(v3,fabs(d3),
v0,fabs(d0),
v1,fabs(d1),
v2,fabs(d2)); break;
// 2 triangles
case 3: slice2tri(v0,fabs(d0),
v1,fabs(d1),
v2,fabs(d2),
v3,fabs(d3)); break;
case 5: slice2tri(v0,fabs(d0),
v2,fabs(d2),
v1,fabs(d1),
v3,fabs(d3)); break;
case 6: slice2tri(v1,fabs(d1),
v2,fabs(d2),
v0,fabs(d0),
v3,fabs(d3)); break;
case 9: slice2tri(v0,fabs(d0),
v3,fabs(d3),
v1,fabs(d1),
v2,fabs(d2)); break;
case 10: slice2tri(v1,fabs(d1),
v3,fabs(d3),
v0,fabs(d0),
v2,fabs(d2)); break;
case 12: slice2tri(v2,fabs(d2),
v3,fabs(d3),
v0,fabs(d0),
v1,fabs(d1)); break;
}
}
// extract 1 triangle from a tetrahedron
// v0 is the cutaway vertex
// d is distance of the respective point to the cutting plane
void slice1tri(const v3d &v0,const double d0,
const v3d &v1,const double d1,
const v3d &v2,const double d2,
const v3d &v3,const double d3)
{
v3d p0,p1,p2;
p0=(d1*v0+d0*v1)/(d0+d1);
p1=(d2*v0+d0*v2)/(d0+d2);
p2=(d3*v0+d0*v3)/(d0+d3);
glBegin(GL_TRIANGLES);
glTexCoord3d(p0.x,p0.y,p0.z);
glVertex3d(p0.x,p0.y,p0.z);
glTexCoord3d(p1.x,p1.y,p1.z);
glVertex3d(p1.x,p1.y,p1.z);
glTexCoord3d(p2.x,p2.y,p2.z);
glVertex3d(p2.x,p2.y,p2.z);
glEnd();
}
// extract 2 triangles (a quad) from a tetrahedron
// v0 is the start point of the cutaway line segment
// v1 is the end point of the cutaway line segment
// d is distance of the respective point to the cutting plane
void slice2tri(const v3d &v0,const double d0,
const v3d &v1,const double d1,
const v3d &v2,const double d2,
const v3d &v3,const double d3)
{
v3d p0,p1,p2,p3;
p0=(d2*v0+d0*v2)/(d0+d2);
p1=(d2*v1+d1*v2)/(d1+d2);
p2=(d3*v0+d0*v3)/(d0+d3);
p3=(d3*v1+d1*v3)/(d1+d3);
glBegin(GL_QUADS);
glTexCoord3d(p0.x,p0.y,p0.z);
glVertex3d(p0.x,p0.y,p0.z);
glTexCoord3d(p1.x,p1.y,p1.z);
glVertex3d(p1.x,p1.y,p1.z);
glTexCoord3d(p3.x,p3.y,p3.z);
glVertex3d(p3.x,p3.y,p3.z);
glTexCoord3d(p2.x,p2.y,p2.z);
glVertex3d(p2.x,p2.y,p2.z);
glEnd();
}
// extract a slice from a tetrahedron
// 2 cases: slice geometry consists of either 1 or 2 triangles
void slice(const v3d &v0, // vertex v0
const v3d &v1, // vertex v1
const v3d &v2, // vertex v2
const v3d &v3, // vertex v3
const v3d &o, // origin of cutting plane
const v3d &n) // normal of cutting plane
{
double d0,d1,d2,d3;
int ff;
d0=(v0-o)*n;
d1=(v1-o)*n;
d2=(v2-o)*n;
d3=(v3-o)*n;
ff=0;
if (d0<0.0) ff|=1;
if (d1<0.0) ff|=2;
if (d2<0.0) ff|=4;
if (d3<0.0) ff|=8;
switch (ff)
{
// 1 triangle
case 1: case 14: slice1tri(v0,fabs(d0),
v1,fabs(d1),
v2,fabs(d2),
v3,fabs(d3)); break;
case 2: case 13: slice1tri(v1,fabs(d1),
v0,fabs(d0),
v2,fabs(d2),
v3,fabs(d3)); break;
case 4: case 11: slice1tri(v2,fabs(d2),
v0,fabs(d0),
v1,fabs(d1),
v3,fabs(d3)); break;
case 8: case 7: slice1tri(v3,fabs(d3),
v0,fabs(d0),
v1,fabs(d1),
v2,fabs(d2)); break;
// 2 triangles
case 3: slice2tri(v0,fabs(d0),
v1,fabs(d1),
v2,fabs(d2),
v3,fabs(d3)); break;
case 5: slice2tri(v0,fabs(d0),
v2,fabs(d2),
v1,fabs(d1),
v3,fabs(d3)); break;
case 6: slice2tri(v1,fabs(d1),
v2,fabs(d2),
v0,fabs(d0),
v3,fabs(d3)); break;
case 9: slice2tri(v0,fabs(d0),
v3,fabs(d3),
v1,fabs(d1),
v2,fabs(d2)); break;
case 10: slice2tri(v1,fabs(d1),
v3,fabs(d3),
v0,fabs(d0),
v2,fabs(d2)); break;
case 12: slice2tri(v2,fabs(d2),
v3,fabs(d3),
v0,fabs(d0),
v1,fabs(d1)); break;
}
}
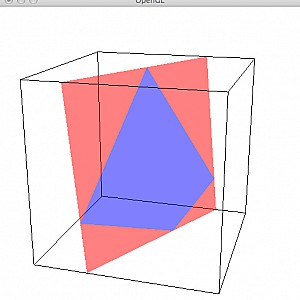
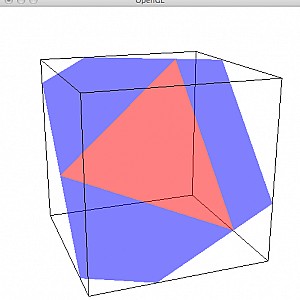
Example decompositions (triangle = red, quad = blue):