C-Uebung

Zusatzaufgabe: Galton-Brett und Binomialverteilung, eine Handübung zum Thema Laufzeitverhalten

← Programm | ● | Zufallszahlen →

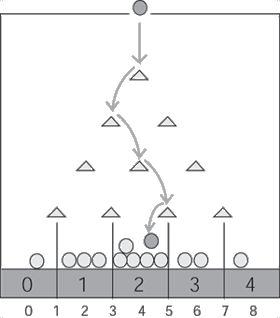
Das Galton Brett ist eine Anordunung bei der Kugeln durch eine regelmässige Anordnung von Stiften fallen. Die Wegverzweigung der Kugel an jedem Stift ist gleichwahrscheinlich. Ein brett der Breite $n$ hat ebensoviele Töpfe, in die eine Kugel fallen kann.

Die Wahrscheinlichkeit P einer Kugel, in einem bestimmtem Topf des Galton Bretts zu landen, ist bestimmt durch die Anzahl der Wege zu diesem Topf geteilt durch die Gesamtanzahl aller Wege.

Die Anzahl der Wege veranschaulicht das sogenannte Pascal’sche Dreieck.

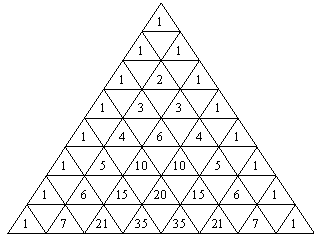
Es gibt genau einen Weg zum Rand. Die Anzahl der Wege an einer beliebigen Position auf dem Brett ist gleich der Summe der Wege zu den zwei Vorgängern (n bezeichnet die Zeile und k die Spalte, der Startwert ist jeweils 0):

$ B(n,0) = 1 $
$ B(n,n) = 1 $
$ B(n,k) = B(n-1, k-1) + B(n-1, k) $

Die Gesamtanzahl der Wege ist $\sum_{i=0}^n B(n,i) = 2^n$.

Damit ist die Wahrscheinlichkeit im k-ten Topf von n Töpfen zu landen $P_k^n=\frac{B(n,k)}{2^n}$.

B(n,k) entspricht dem sogenannten Binomialkoeffizienten.

Obige Definition des Binomialkoeffizienten is rekursiv, die bekanntere iterative Definition ist:

$ \displaystyle{ B(n,k) = n \choose k = \prod_{j=1}^k \frac{n+1-j}{j} = \frac{n!}{k! (n-k)!} } $

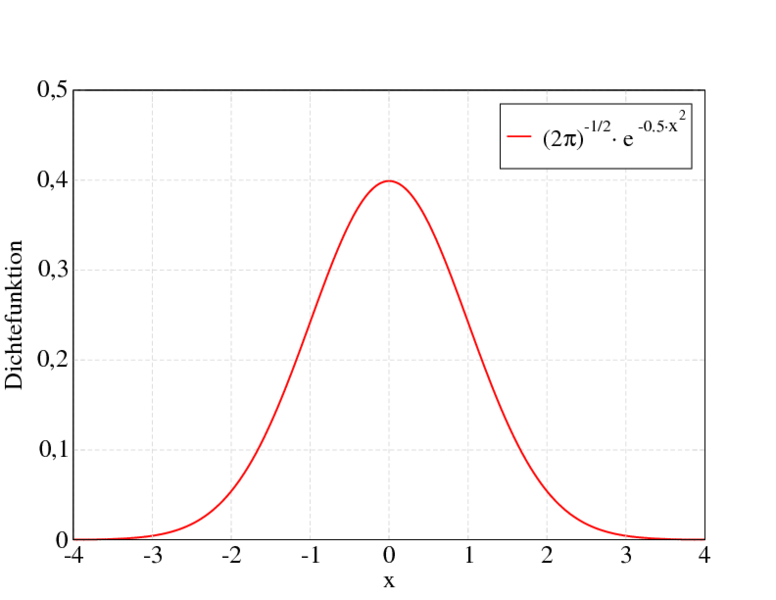
Damit entspricht die Wahrscheinlichkeitsverteilung der Kugeln in den Töpfen der Binomialverteilung. Für $n \to \infty$ konvergiert diese gegen die Normalverteilung mit der Eulerschen Normalverteilungsfunktion $\phi(x)$.

$ P_k^n \approx \frac{2}{\sqrt n} \phi((k-\frac{n}{2})\frac{2}{\sqrt n}) $
$ B(n,k) \approx \frac{2^{n+1}}{\sqrt n} \phi((k-\frac{n}{2})\frac2{\sqrt n}) $
$ \phi(x) = \frac{1}{\sqrt{2\pi}} e^{-\frac{1}{2}x^2} $

Schreiben Sie ein Programm, welches den Binomialkoeffizienten rekursiv und iterativ zu einem gegebenen $n$ und $k$ ermittelt.

Q Was kann man über das Laufzeitverhalten (Anzahl Operatoren und Aufrufe) der iterativen und rekursiven Variante sagen, d.h. welcher Faktor dominiert die Laufzeit?

Q Vergleichen Sie die Laufzeit der beiden Varianten, indem Sie die Laufzeiten für die Berechnung von B(20,10) messen.

Q Berechnen Sie das Fehlerquadrat der exakten [iterativen] und der genäherten Berechnung (via Normalverteilungsfunktion) von B(20,10).


← Programm | ● | Zufallszahlen →

Options: