Computergrafik-Uebung

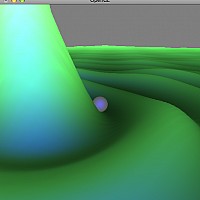
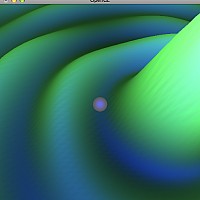
Animation

●?

Optionale Zusatzaufgabe: Animation

Animieren Sie eine Kugel, die sich auf der Oberfläche der dargestellten Funktion bewegt in Anlehnung an den Spieleklassiker “Marble Madness”.

MarbleMadnessNES

Simulieren Sie dazu inkrementell von Zeitpunkt zu Zeitpunkt die Bewegung einer Punktmasse, die mit einer Beschleunigung $\vec{a}$ vorangetrieben wird:

$ \vec{a} = (0,0,-g)^T $

Die Gravitationskonstante sei g, die aktuelle Position der Punktmasse zum Zeitpunkt t sei $\vec{p}$ und $\vec{v}$ die Geschwindigkeit:

$ \vec{v}' = \vec{v}+\vec{a}\Deltat $
$ \vec{p}' = \vec{p}+\vec{v}\Deltat $

Dadurch befindet sich die Kugel im freien Fall. Verwenden Sie gluSphere() zum Zeichnen der Kugel an der Position $\vec{p}$.

Stellen Sie sicher, dass die Kugel beim Aufprall auf der Oberfläche diese nicht durchdringt. D.h. der Abstand des Kugelschwerpunkts von der Oberfläche darf nicht kleiner als der Kugelradius $r$ werden:

$ f(p_x,p_y)+r \gt p_z : \quad p_z = f(p_x,p_y)+r $

Durch den Aufprall der Kugel auf einer Oberfläche kehrt sich die Geschwindigkeitskomponente, die senkrecht zur Oberfläche ist, um, d.h. der Geschwindigkeitsvektor $\vec{v}$ wird an der Oberflächennormale $\vec{n}$ reflektiert:

$ \vec{v}' = \vec{v}-2(\vec{v}\cdot\vec{n})\vec{n} $

Gleichzeitig wird die Sprungbewegung nicht-elastisch gedämpft:

$ \vec{a} = -c_{d}|\vec{v}\cdot\vec{n}|\vec{n} $

Hinweis: Verwenden Sie als Hilfsmittel zur Darstellung von 3D-Vektoren die C++ Klasse v3d.


Shot1 Shot2 Shot3


FĂĽr Fortgeschrittene: Verwenden Sie eine 3D Textur (z.B. eine prozedurale 3D Marmor Textur) zur Texturierung der Murmel und animieren Sie das Rollen der Kugel. Die Rotationsachse und Drehfrequenz ist:

$ \vec{r} = \vec{v}\times\vec{n}, \quad f = \frac{|\vec{v}|}{2\Pir} $

Options: