Open GL Coordinate Systems
← OpenGL ModelView Transformations | ● | OpenGL Matrix Stack →
The 3D objects are modelled in local coordinates and put into world coordinates via rigid body transformations (rotation and translation).
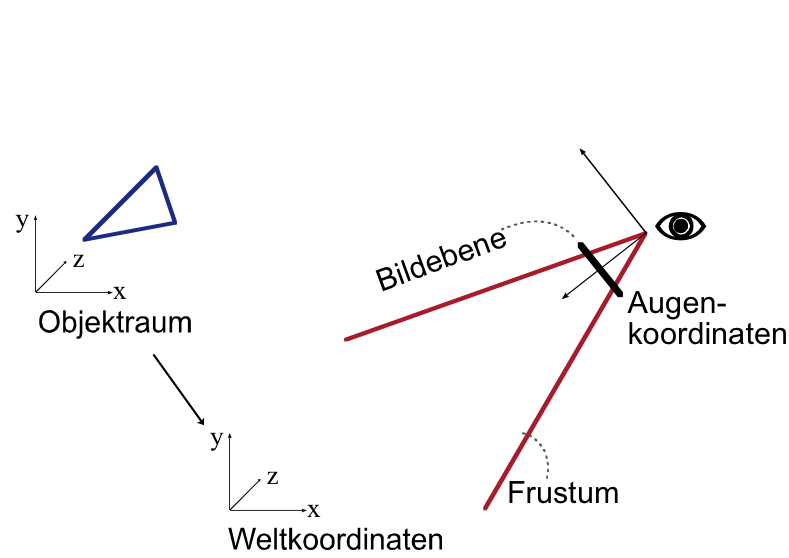
All rigid body transformations (or affine transformations) can be described by 4×4 matrices in homogene coordinates. So an arbitrary sequence of affine transformations can be described by a single 4×4 matrix which is the multiplication of the respective 4×4 matrices of all single transformations.
For example to rotate an object by 90 degrees around the vertical axis and translate it left we use:
glRotatef(90,0,1,0);
The order of transformations is read from bottom to top.
Initially the camera position and view direction is the origin of the world coordinate system looking along the negative z axis. The camera coordinate system is determined by another 4×4 transformation:
glLoadIdentity();
gluLookAt(0,0,10, // camera position
0,0,-10, // look at position
0,1,0); // up vector
So the most fundamental task of the graphics pipeline is to transform the incoming vertices with a single combined 4×4 matrix (the so called combined model view matrix) which defines both the object position in world space and the camera position under which the world scene is displayed.
The camera lens type is determined by the so called perspective transformation matrix:
glLoadIdentity();
gluPerspective(90, // vertical field of view (fovy)
1, // window aspect
1, // near plane distance
10); // far plane distance
← OpenGL ModelView Transformations | ● | OpenGL Matrix Stack →