VolumeRendering
Emission
← Integration with OpenGL | ● | Emission and Absorption →
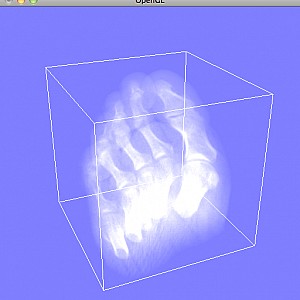
Assumption: no absorption, just emission
- Emitted light is accumulated on the viewing rays
- Accumulated intensity is linear proportional to the traveled ray length
$ TF_{RGB}(s) = \mu_E s $
$ I = I_0 + \int_{t=0}^1 \mu_E s(t) dt $
Numerical integration step:
$ I' = I + \mu_E s(t) \Delta t $
Realization of numerical integration with OpenGL: Numerical integration by view-aligned slicing with slice distance $\Delta t$ and add-operator with constant vertex color $(\mu_E \Delta t, \mu_E \Delta t, \mu_E \Delta t)$ and modulation of vertex color with 3D-texture lookup of $s(t)$.
Ambient background emission needs to be disabled.
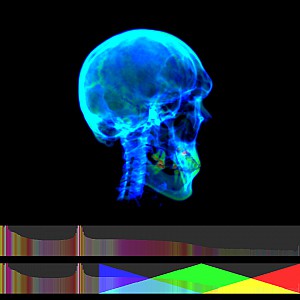
Non-linear transfer function $TF_E=\kappa(s(t))$ allows coloring of specific materials based on their scalar value (using a TF Editor):
Colored via transfer function:
Advantages:
- commutative
- colors
Disadvantages:
- still no depth perception
- emission gets saturated quickly
Vertex color:
glColor4f(muE*dt,muE*dt,muE*dt,0);
3D texture modulation:
glEnable(GL_TEXTURE_3D);
glTexEnvi(GL_TEXTURE_ENV,GL_TEXTURE_ENV_MODE,GL_MODULATE);
glTexEnvi(GL_TEXTURE_ENV,GL_TEXTURE_ENV_MODE,GL_MODULATE);
Add-operator with OpenGL-blending:
glBlendFunc(GL_ONE,GL_ONE);
glEnable(GL_BLEND);
glEnable(GL_BLEND);