CGExercises

CG Exercise #06

Computergraphik Ãœbungsblatt #06

OpenGL Tutorial: Hierarchische Modellierung


OpenGL: Roboterarm

Aufgabe 6.1: Roboterarm, Präliminarien


Verwendete Meshes

Starten Sie mit dem Quelltext robot.cpp.

Dieses Programm zeichnet einen Würfel und eine Kugel, und erlaubt die Höhe des Würfels mit Hilfe von Tastendrücken zu verändern. Machen Sie sich mit dem Quelltext vertraut, und analysieren Sie ihn.

Materialien:

Aufgabe 6.2: Roboterarm, Grundplatte

Bisher wird ein Würfel und eine Kugel gezeichnet. Jetzt wollen wir aus diesen einfachen graphischen Grundkörpern einen Roboterarm zusammenbauen. Die Würfel werden die Armsegmente, die Kugeln die Gelenke usw. Wie der Arm des Roboters im Raum steht, wird durch die jeweiligen Drehwinkel an den Gelenken (d.h. den Roboterachsen) bestimmt.

Damit wir die einzelnen Elemente unabhängig voneinander bewegen können, werden wir den Arm mittels hierarchischer Modellierung aufbauen. Und um die einzelnen Elemente besser unterscheiden zu können, benutzen wir verschiedene Farben für die einzelnen Elemente.


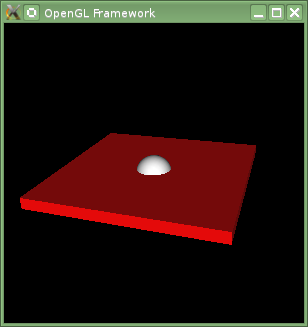
Skalierte Basisplatte

Zeichnen Sie als erstes eine Grundplatte, in deren Mitte der Roboter Stück für Stück aufgebaut wird. Skalieren Sie also den Würfel mit Hilfe einer Skalierungsmatrix (mat4::scale()) vor allem in der z-Achse so, dass er relativ flach wird.

In der Mitte zeichnen Sie eine Kugel, die das 1. Drehgelenk des anschließenden 1. Armsegments darstellen soll. Dafür benötigen wir eine ModelView-Matrix für ein lokales Koordinatensystem, welches in der Mitte der Basisplatte liegt. Alle weiteren lokalen Koordinatensysteme der Armsegmente bauen darauf auf. Diese Matrix berechnen wir daher zuerst und speichern diese in der Variable $MV$.

Dann setzen wir die ModelView-Matrizen vor dem Zeichnen der entsprechenden graphischen Primitve mit Hilfe von lglModelView(), da jedes Primitiv eine andere ModelView-Matrix nutzt. Die Projektions-Matrix ändert sich nicht, und muss daher auch nicht neu mittels lglProjection() gesetzt werden.

Aufgabe 6.3: Roboterarm, Erstes Segment


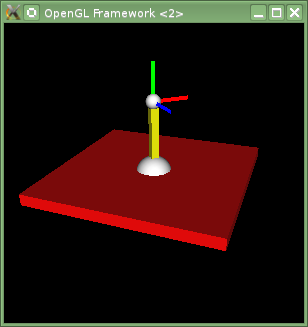
Erstes Segment

Zeichnen Sie dann das erste Armsegment. Dafür müssen Sie aufbauend auf der bisherigen ModelView-Matrix $MV$ weitere Transformationen durchführen, bevor Sie den nächsten Quader zeichnen. Sie brauchen dafür kein neues Objekt, Sie können das bereits existierende einfach ein zweites Mal zeichnen. Denken Sie daran, dass die Zeichenroutine das Koordinatensystem in der Mitte des Würfels erwartet, und dass der Würfel die Einheits-Kantenlänge 1 hat. Für das erste Segment wird der Würfel in der Höhe skaliert und um die Hälfte der Armlänge nach oben transliert.

Zeichnen Sie dann wieder ein Gelenk bzw. eine Kugel. Auch dieses Gelenk muss wieder an die richtige Stelle am Ende des Arms geschoben werden. Berechnen Sie keine Teilmatrizen doppelt, d.h. verwenden Sie wann immer möglich Matrizen, die bereits vorher berechnete wurden. Wir können die MV Matrizen bis auf die abschließende Skalierungsmatrix wiederverwenden, d.h. diese Teil-Matrix des letzten Elements ist die Basis für das nächste Element.

Drehen Sie nach obigem Prinzip nun den Arm um 45 Grad um seine eigene Achse (d.h. die Y-Achse).

Aufgabe 6.4: Lokales Modellierungs-Koordinatensystem

Es ist wichtig, sich zu erinnern, wo sich das jeweilige Koordinatensystem befindet, und welche Achse wohin zeigt - zeichnen Sie daher ein lglCoordSys-Objekt am jeweils oberen Ende des Arms.

Aufgabe 6.5: Rotation per Tastendruck

Ermöglichen Sie dem Arm, sich um seine eigene Achse zu drehen, wenn Sie z.B. die Tasten ‘q’ und ‘w’ drücken. Speichern Sie den Drehwinkel in einer Instanz-Variablen “angle”, und benutzen Sie ihn in der renderOpenGL()-Routine, um die ModelView-Matrix entsprechend zu modifizieren.

Aufgabe 6.6: Weitere Segmente


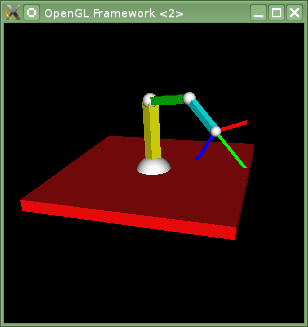
Roboterarm mit 3 Segmenten

Analog zu den vorherigen Schritten bauen Sie nun jeweils abwechslend ein weiteres Gelenk und ein weiteres Armsegment an, um zwei weitere Armsegmente zu realisieren. Diesmal rotieren die Armsegmente an den Gelenken um die X-Achse. Den Winkel stellen Sie mit passenden Tasten ein. Vergessen Sie nicht, eine andere Farbe für diese Armsegmente zu verwenden.


Aufgabe 6.7: Greifer (Optional)


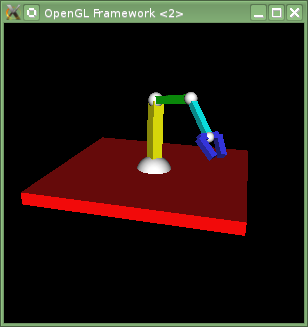
Roboterarm mit Greifer

Bauen Sie an das letzte Roboterarmsegment jetzt einen Greifer an, der sich um sein “Handgelenk” drehen kann, und seine Greiferfinger öffnen und schließen kann.


Hausaufgaben bis zum nächsten Praktikum

Musterlösung: Bitte stellen Sie Ihre Musterlösung aus dem Praktikum kurz vor.

Diese Hausaufgabe ist teilweise eine Rechercheaufgabe: Bitte googlen oder schlagen Sie entsprechend in der Vorlesung nach, wenn Sie manche Begriffe noch nicht kennen!

1. OpenGL / Meshes:
In welchem Format sind Meshes in einer OBJ Datei gespeichert in Bezug auf folgende Schlagwörter:

  • tri-stripping
  • indexed face set
  • triangle orientation (clockwise=cw / counter-clockwise=ccw)
  • normal orientation (inside, outside)
  • texture coordinates (range)

Tipp: Schauen Sie eine OBJ-Datei an - dies ist eine “lesbare” Text-Datei! Analysieren Sie deren Struktur und Inhalt!

2. OpenGL / Texturkoordinaten:
Ein Rechteck mit den Bildschirmkoordinaten (0 50), (100 50), (100 0) und (0 0) wird mit einer Textur mit einem 4×4 Schachbrettmuster gefüllt; dabei haben die 4 Eckpunkte die Texturkoordinaten (0.5 1), (1 0.5), (0.5 0) und (0 0.5).

  1. Skizzieren Sie das entstehende texturierte Rechteck. Zeichen Sie dazu erst die ganze Textur in Texturkoordinaten, und überlegen Sie Sich in dieser Zeichnung, welcher Teil der Textur überhaupt verwendet wird.
  2. Welche Texturkoordinate ergibt sich in der Mitte des Rechtecks?

3. OpenGL / Mip-Mapping:

  1. Recherchieren Sie das Prinzip des sog. “Mip-Mapping”
  2. Wieviele Stufen hat die MipMap-Pyramide für obige Textur?
  3. Welche Farbe ergibt sich für die letzte Stufe?

Options: