Computergraphik Übungsblatt #03

Blender Tutorial: Rigging & Animation

Animieren mit Blender (Blender Teil #3)

In diesem Praktikumsteil befassen wir uns mit der Animation von realen Objekten. Hierzu wird in Blender hauptsächlich die sog. Free-Form-Deformation mittels Key-Frames eingesetzt:

Aufgabe 3.1: Rigging - Bone-Hierarchien

Die Animation in Blender geschieht hauptsächlich mit Hilfe von Rigging, d.h. der Definition eines Knochengerüstes (Rig).

Das Rig gibt die Bewegung einzelner Teile der Objekte vor. Hierbei helfen hierarchische Beziehungen zwischen den Teilen der Objekte bei der Vereinfachung einer entsprechenden Animation.

Bitte erstellen Sie ein Knochengerüst (Rig, Armature, Shift+A) für eines der vorher modellierten Objekte, so dass das Rig eine Deformation der einzelnen Meshbereiche gemäß der Animation bewirkt.

Mit dem “Skin” Modifier können Sie recht einfach 3D-Strichfiguren erstellen. Gleichzeitig ermöglicht dieser die Ableitung eines Rigs per Knopfdruck. Wenden Sie dazu jedoch ggf. den Mirror Modifier an. Wenn Sie ein komplett neues Rig (Armature) erstellen, dann müssen Sie das zu animierende Mesh als Kind der Amature (STRG + P im Object mode) zuweisen. Sorgen Sie für genügend Gelenke zum Animieren. Lassen Sie Blender automatisch das aufwendige Skinning durchführen, indem für jeden Bone die zugehörigen Vertices (Vertex Groups) ermittelt und zugewiesen werden (Armature Deform - With Automatic Weights).

Aufgabe 3.2: Animation - Objectmode und Posemode

Animieren Sie bitte das Rig für eines Ihrer Objekte aus der vorherigen Übung. Für die allgemeine, rigide Objektbewegung können Sie die Armature im Object mode über Keyframes animieren.

Um feinere Deformationen (z.B. Veränderung der Extremitäten) zu animieren, erstellen Sie entsprechend Keyframes im Posemode der Armature.

Denken Sie auch an die Animation der Kamera! Das funktioniert genauso wie die Animation des Rigs im Object mode mithilfe von Keyframes. Schaffen Sie es eine kleine Geschichte mit einfachen Bewegungen zu erzählen?

Aufgabe 3.3: Rendering - Die Animation als Videodatei ausspielen

Nun geht es abschließend ums sog. Rendering, d.h. die Erzeugung eines Films!

Bitte rendern Sie die Animation unter Verwendung von Globaler Beleuchtung mithilfe der (a) Cycles und (b) EEVEE Renderengine. Beachten Sie bitte hierbei, dass Ihre Kamera über die gesamte Animation hinweg die passende Ausrichtung hat und dass das Rendern u. U. sehr lange dauern kann… .

Um bei etwaigen Abstürzen die Arbeit nicht zu verlieren, rendern Sie die Animation zunächst als Bildsequenz (z.B. .jpg oder .png) und fügen diese im Video-Editor von Blender wieder zu einem Film zusammen, den Sie dann als Videodatei (z.B. .mp4) ausgeben.

Wenn sie bis hierher gekommen sind, haben Sie die Grundlagen der Computergraphik in Blender erlernt und gleichzeitig Ihren ersten Kurzfilm erstellt. Herzlichen Glückwunsch!

Hausaufgaben bis zum nächsten Praktikum

Musterlösung: Bitte stellen Sie Ihre Key-Frame Animation aus dem Blender-Praktikum kurz vor.

1. Blender-Projekt
Bereiten Sie als Blender-Team eine Folie vor, auf der Sie Ihr Blender-Projekt kurz beschreiben und Ihr Team z.B. als Gruppenfoto vorstellen! Laden Sie diese Folie bis zur nächsten Übungsstunde ins Protokoll-Uploadverzeichnis hoch (Format: BlenderProject-XYZ.pdf).

2. Theorie:

1. BRDF:
   Zeichnen Sie die BRDF von einer Spiegelkugel, einer Plastikkugel und einer schwarzen und einer weißen matten Kugel (analog zu den Illustrationen in der Vorlesung)!
2. Globale Beleuchtung:
   Nehmen Sie an, dass Ihre Szene aus einem Raum mit zwei Plastikwürfeln besteht. Zeichnen Sie beispielhaft die Lichtwege, die für die folgenden globalen Beleuchtungsmodelle relevant sind (zeichnen Sie der Einfachheit halber nicht dreidimensional):
   1. Raytracing
   2. Radiosity (im Kontext von Baking)
   3. Ambient Occlusion (im Kontext eines Rasterisierers)
   4. Monte-Carlo (im Kontext eines Path-Tracers)
3. Optional: Kaustik
   Ganz dumm gefragt: Wieso lassen sich Kaustiken weder mit Raytracing noch mit Radiosity darstellen? Was ist überhaupt eine Kaustik? Begründen Sie Ihre Antwort zeichnerisch anhand der auftretenden Lichtpfade!
4. Rendering Backend:
   1. Welches prinzipielle Rendering-Verfahren kommt bei Eevee und Cycles zum Einsatz?
   2. Welche Unterschiede ergeben sich dadurch in der Bildqualität?
   3. Gibt es weitere Unterschiede?

3. Blender / Texturierung:

1. Erklären Sie bitte, wie es funktioniert, dass zweidimensionale Bilder auf dreidimensionalen Objekten dargestellt werden können. Welche zwei Dinge benötigt man unbedingt, damit dies funktioniert?
2. Was ist der Unterschied zwischen Welt-, Objekt- und Texturkoordinaten? Welches konkrete kartesische Welt-Koordinatensystem verwendet Blender im Gegensatz zu OpenGL? Das heißt, wie sind die Achsen der Koordinatensysteme orientiert?
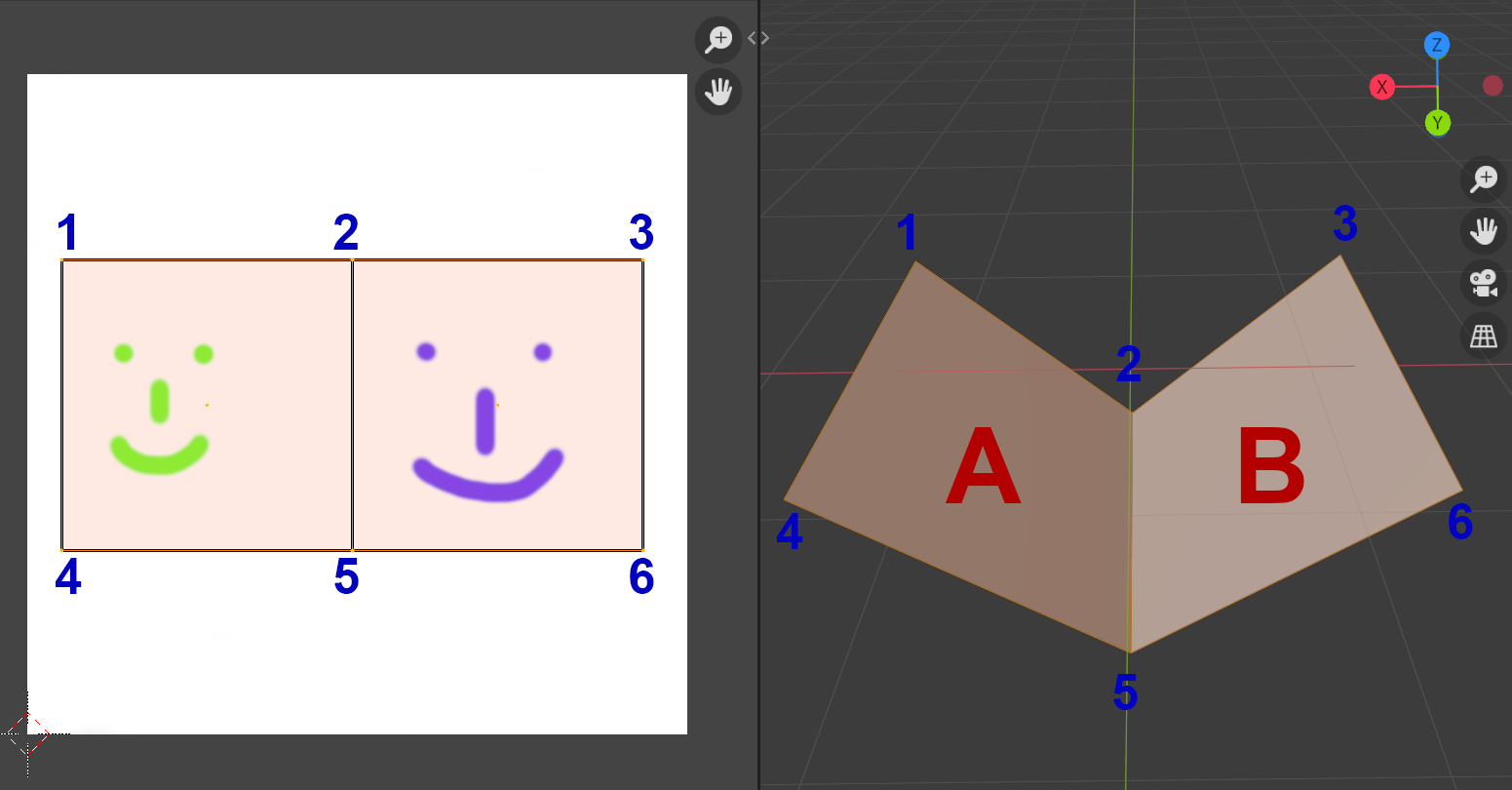
3. In folgendem Bild ist die Zuordnung von 3D Raum zum 2D Bildraum gegeben (Zahlen 1 bis 6). Beschreiben Sie bitte welche Formen jeweils auf den Flächen A und B zu sehen sind, wenn in Blender die Materialien richtig definiert und dargestellt werden.