Computergraphik Übungsblatt #05

OpenGL Tutorial: Modeling & Viewing

OpenGL & MVP

Aufgabe 5.1: Präliminarien

Programmiervorlage:

OpenGL Cheat Sheet

Wir beginnen damit, einen einfachen Würfel wie in der Hausaufgabe zu zeichnen. Sie sollten dazu eine Kopie des Programms bzw. Quelltextes in einem neuen Verzeichnis anlegen (siehe Cheat-Sheet). Eine Kopie zu erstellen, ist auch die empfohlene Vorgehensweise für alle weiteren Übungen. Das Hauptprogramm ersetzen wir durch den Quelltext cube.cpp, der bereits einen vorgefertigten Würfel darstellt.

Materialien:

• cube.cpp
• OpenGL Cheat Sheet
• OpenGL Programming Guide
• Vorlesung: MVP Anwendungs Beispiel

Aufgabe 5.2: Aufwärmen mit der GLM (bzw. GLSLMath)

Definieren Sie mit der GLM bzw GLSLmath (siehe Cheat Sheet) den homogenen 3D Punkt bzw. Vertex $v = (0,0,-1,1)$ und geben Sie ihn auf der Konsole aus (mit dem << operator).

Den Vertex $v$ kann man auch etwas hübscher mit glslmath::print(...) ausgeben.

Berechnen Sie die sog. aspect-ratio, d.h. das Seitenverhältnis des Framebuffers (wie z.B. 16:9 bei FHD) und geben Sie dieses Verhältnis ebenfalls aus.

Tipp: Breite und Höhe des Framebuffers → width() bzw. height()

Aufgabe 5.3: Spaß haben mit dem Trackball des Frameworks

Das Framework hat die Möglichkeit, einen Trackball zur Verfügung zu stellen, bei dem man mit der Maus das dargestellte Objekt “greifen” und rotieren kann.

Dazu stellt das Framework eine Rotations- bzw. Modellierungsmatrix $M_{manip}$ zur Verfügung, die von der lglGetManip() Funktion zurück geliefert wird. Diese speichern wir uns in einer Variable ab:

Nun multiplizieren wir den Vertex $v$ erst einmal mit dieser Modellierungsmatrix $M_{manip}$ und geben beides fortlaufend mit glslmath::print(...) aus.

Bauen Sie den Trackball nun in Ihr Programm ein, so dass Ihr Objekt mit dem Trackball bzw. der Modellierungsmatrix $M_{manip}$ rotiert wird. Dazu nehmen wir an, dass die View-Matrix $M_V$ momentan noch die Einheitsmatrix ist, so dass die Modelview-Matrix $M_{MV}$ der Matrix $M_{manip}$ entspricht. Diese Modelview-Matrix verwenden wir nun für die Grafikkarte. Dazu übergeben wir dem Befehl lglModelView(...) eine entsprechende Matrix.

Tipp: Der Trackball skaliert auch (mit dem Mausrad).

Aufgabe 5.4: MVP Berechnen

Wir verwenden eine Kamera

Nun berechnen wir die restlichen Teilmatrizen der MVP-Matrix selber mit GLSLmath:

Projektions-Matrix / Perspektive:

1. Das View-Frustum habe einen vertikalen Blickwinkel von 90 Grad, ein Bildseitenverhältnis von 16:9 und $near = 1$ bzw. $far = 10$. Stellen Sie Sich vor, dass eine Einheit z.B. einem Meter entspricht!
2. Berechnen Sie die entsprechende Projektionsmatrix $M_P$ mit Hilfe von GLSLmath via mat4::perspective und geben Sie sie aus. Beachten Sie außerdem, dass das korrekte Seitenverhältnis für $M_P$ verwendet wird!
3. Wofür ist die −1 in der 3ten Spalte und 4ten Zeile zuständig?

Model-View-Projection-Matrix:

1. Wir verwenden dieselbe Modellierungsmatrix $M_M$ und die dieselbe Viewing-Matrix $M_V$ wie in der Hausaufgabe!
2. Berechnen Sie diese Matrizen nun mit Hilfe von GLSLmath, d.h. wir verwenden mat4::lookat für $M_V$ und eine Kombination von mat4::translate und mat4::rotate für $M_M$.
3. Berechnen Sie nun die homogene 4×4 Model-View-Matrix $M_{MV}$ mit GLSLmath, d.h. berechnen Sie die Gesamtmatrix $M_{MV}$ durch Multiplikation der entsprechenden Teilmatrizen!
4. In welcher Reihenfolge müssen die obigen Matrizen multipliziert werden?
5. Geben Sie das Resultat für beide Matrizen aus und vergleichen Sie mit der Hausaufgabe!
6. Berechnen Sie schließlich die konkrete MVP bzw. $M_{MVP}$ und geben Sie sie endlich aus!

Aufgabe 5.5: MVP anwenden

Würfel mit MVP

Verwenden Sie nun die obige MVP-Matrix zur perspektivischen Darstellung Ihres Objekts bzw. Würfels. Dabei ist die Gesamtmatrix so aufgeteilt, dass $M_P$ mit lglProjection(...) geladen wird und $M_{MV}$ mit lglModelView(...). Der Grund dafür ist, dass sich erstens die Projektionsmatrix für einen Frame nicht ändert und zweitens $M_{MV}$ später noch für Beleuchtungsberechnungen benötigt wird.

Aufgabe 5.6: MVP mit Trackball

Verwenden Sie außerdem wieder die Modellierungsmatrix $M_{manip}$ des Trackballs als zusätzliche Modellierungsmatrix. An welcher Stelle muss diese Matrix in die Modellierungstransformation eingefügt werden, damit das Objekt rotiert wird?

Aufgabe 5.7: Meshes und Koordinatensysteme

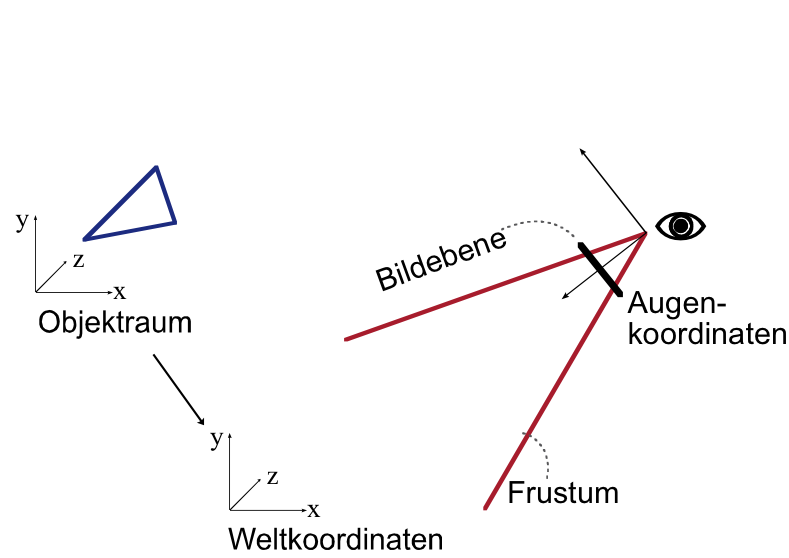
OpenGL Koordinatensysteme

Das Framework bietet wie Blender vorgefertigte Meshes bzw. VBOs für die Darstellung von Kugeln, Pyramiden, Tori etc. (siehe Cheat Sheet → VBOs). Diese sind alle auf eine Einheitsgröße normiert, so dass sie sich mit einer Skalierungsmatrix S einfach auf eine bestimmte Größe skalieren lassen.

Insbesondere bietet das Framework das Mesh lglCoordSys als Koordinatensystemkreuz mit drei verschiedenfarbigen Achsen. Stellen Sie damit das lokale Koordinatensystem Ihres Objektes dar, d.h. das Koordinatensystem, welches mit dem Trackball rotiert wird.

Verwenden Sie dieses Mesh ebenfalls, um das System der Weltkoordinaten darzustellen. Berechnen Sie dazu zuerst eine weitere entsprechende MVP-Matrix für dieses zusätzliche Koordinatensystem. Da die Projektions-Matrix gleich bleibt, reicht es aus, nur eine weitere entsprechende weitere Model-View-Matrix zu berechnen und via lglModelView(...) auf die Graphikkarte zu laden.

Gehen Sie also nach folgendem Muster vor:

Welche Anpassungen müssen vorgenommen werden, damit das Weltkoordinatenkreuz sichtbar wird?

Aufgabe 5.8: Weitere Meshes (Empfohlen)

Bauen Sie jetzt weitere Objekte bzw. Meshes in Ihr Programm ein. Zeichnen Sie z.B. ein paar Kugeln, Tori, Teapots etc. und färben Sie diese Objekte unterschiedlich ein (via lglColor()).

Aufgabe 5.9: Experimentieren (Optional)

Experimentieren Sie mit der Reihenfolge der Rotationen und Translationen und der Skalierung verschiedener Meshes.

Lassen Sie ein Objekt um sich selber rotieren und lassen Sie ein Objekt um den Weltursprung rotieren.

Experimentieren Sie z.B. auch mit der nicht-uniformen Skalierung eines Würfels zu einem Quader.

Aufgabe 5.10: MVP im Shader (Optional)

Ergänzen Sie den Code um einen Shader bzw. bauen Sie in Ihren Code einen Shader-Editor ein. Dazu benötigen Sie die folgenden zusätzliche Zeilen:

Im Globalen Namensraum:

GLuint prog_id;
const char shader[] = "";

In der Methode initializeOpenGL():

prog_id = lglCompileGLSLProgram(shader);
create_lgl_Qt_ShaderEditor("shader", &prog_id);

In der Methode renderOpenGL():

lglUseProgram(prog_id, false);

Der Shader Editor startet mit dem denkbar einfachsten Programm, dem sog. Plain-Shader.

Überlegen Sie Sich: Aus welchen zwei Bestandteilen besteht dieser Plain-Shader? Welche Stufe der Graphik-Pipeline repräsentieren diese und welche Stufe befindet sich dazwischen? In welcher Stufe wird mit der MVP multipliziert und wie häufig? Wie häufig wird der andere Bestandteil verwendet? Dies ist zum Verständnis der weiteren Übungen relevant!

Aufgabe 5.11: Sonnensystem (Optional)

Ein nettes Spielzeug

Versuchen Sie, mit geigneten Rotationen und Translationen die Objekte wie ein Planetensystem (Sonne/Erde/Mond/Satellit/Hai) umeinander rotieren zu lassen. Fangen Sie mit der Sonne an, d.h. platzieren Sie eine gelbe Kugel im Ursprung der Weltkoordinaten.

Tipp: Bei vielen Objekten bzw. bei vielen lokalen Koordinatensystemen kommt man schnell durcheinander. Speichern Sie Sich daher die jeweils letzte funktionierende Programmversion als Sicherheitskopie ab.

Hausaufgaben bis zum nächsten Praktikum

Musterlösung: Bitte stellen Sie Ihre Musterlösung aus dem Praktikum kurz vor.

1. Zusammengesetzte Transformationen:

1. Die Rotation um einen Punkt (der nicht der Ursprung ist) ist eine aus drei Teil-Transformationen zusammengesetzte Transformation (siehe Vorlesung). Berechnen Sie im zwei-dimensionalen Raum mit homogenen Koordinaten die Rotation des Punktes P mit den Koordinaten (4, 1) um 90 Grad im Uhrzeigersinn um den Punkt A mit den Koordinaten (2, 2) wie folgt:
2. Stellen Sie die drei 3×3 Teil-Transformationsmatrizen auf.
3. In welcher Reihenfolge müssen die obigen Matrizen multipliziert werden?
4. Berechnen Sie durch Matrixmultiplikation die 3×3 Matrix, mit der die gesamte Transformation durchgeführt werden kann.
5. Anschließend transformieren Sie den Punkt P, und überprüfen zeichnerisch, ob das Ergebnis stimmt.

Ein netter alter Ausziehtisch

2. Hierarchische Modellierung / Theorie:
Ein Tisch besteht aus einer Arbeitsplatte und vier Beinen. Die Beine sind getrennt von der Tischplatte modelliert. Dabei sei $M_P$ die Projektion, $M_V$ die View-Transformation, $M_T$ die Modellierungstranformation, welche die Position (und Orientierung) des Tisches in der Welt beschreibt, und $M_{B_x}$ die vier Modellierungstransformationen, die beschreiben, wie man von der Tischposition zur Position des x-ten Beines kommt.

1. Zeichnen Sie den dazugehörigen Szenengraphen!
2. Und beschreiben Sie nun, wie die ModellViewProjection-Matrizen prinzipiell aufgebaut werden müssen, um die einzelnen 5 Elemente zu rendern!

3. Hierarchische Modellierung / Pseudo-Coding:
Wie würde die vorhergehende Aufgabe mit Pseudocode aussehen? Nehmen Sie an, Sie haben die Funktionen zeichneTischplatte() und zeichneTischbein() zur Verfügung und die benötigten Transformationen stehen schon in den Matrizen $M_V$, $M_T$, $M_{B_1}$, $M_{B_2}$, $M_{B_3}$ und $M_{B_4}$ zur Verfügung. Beschreiben Sie die Darstellung des modellierten Tisches eine Abfolge von Funktionsaufrufen mit den jeweils dafür benötigten konkreten zusammengesetzten MV-Matrizen. Anmerkung: Wir können die P-Matrix außer acht lassen, da sie sich über die ganze Zeit nicht ändert. Wir können die V-Matrix aber nicht außer acht lassen, da sie sich von Frame zu Frame ändern kann. Wir betrachten daher also nur die jeweiligen MV-Matrizen.