Computergrafik
Parametrische Oberfl├Ąchen
← Probleme von Dreiecksgittern | ● | Bezier Curves →
- High-Level Repr├Ąsentation von Kurven bzw. Oberfl├Ąchen
- z.B. Splines, NURBS
- Polynomial oder rational
- 1D Polynom: $p(x) = 1 -2x +3x^2 -10x^3$
- 2D Polynom: $p(x,y) = 1 + x -2y +3x^2 -xy -2y^2 + x^3$
- rational: $p(x) = \frac{x^2+4x-1}{2x+1}$
- Global oder st├╝ckweise zusammengesetzt
- Global:
- $p(x) = a^n x^n + a^{n-1} x^{n-1} + ... a^1 x^1 + a^0 x^0$
-
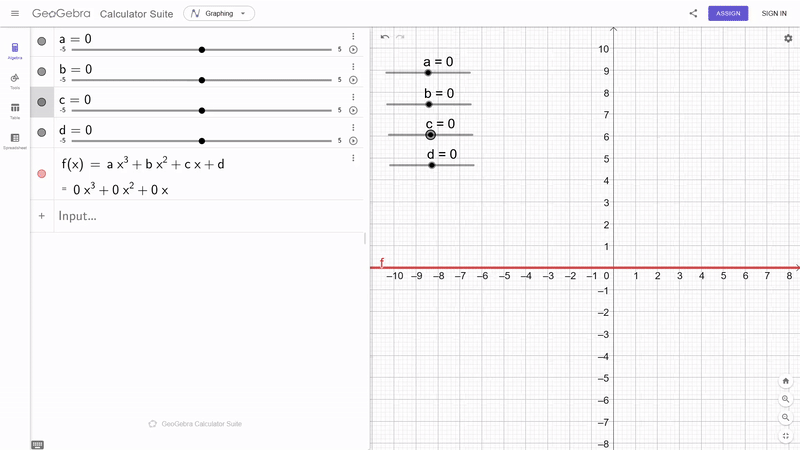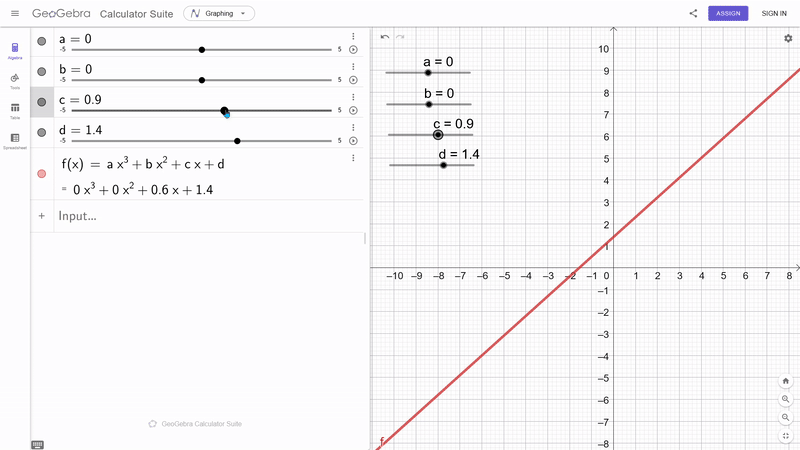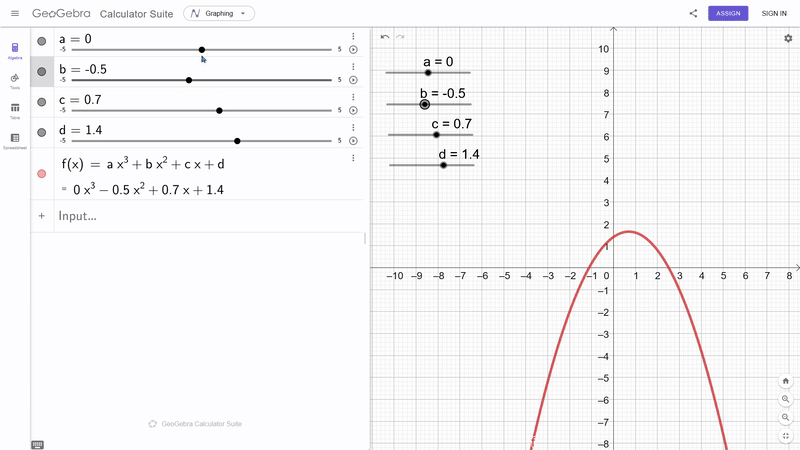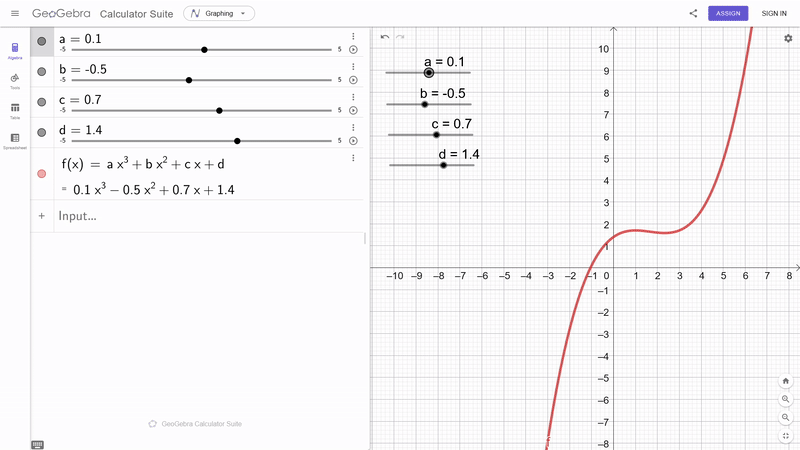
- St├╝ckweise:
- $p_1(x) = 2x^3 -3x^2 + x$ f├╝r $x \in [0,1]$
- $p_2(x) = -x^3 +4x^2 - x$ f├╝r $x \in [1,2]$
- $p_3(x) = 2x^3 -3x^2 + x$ f├╝r $x \in [2,3]$
-
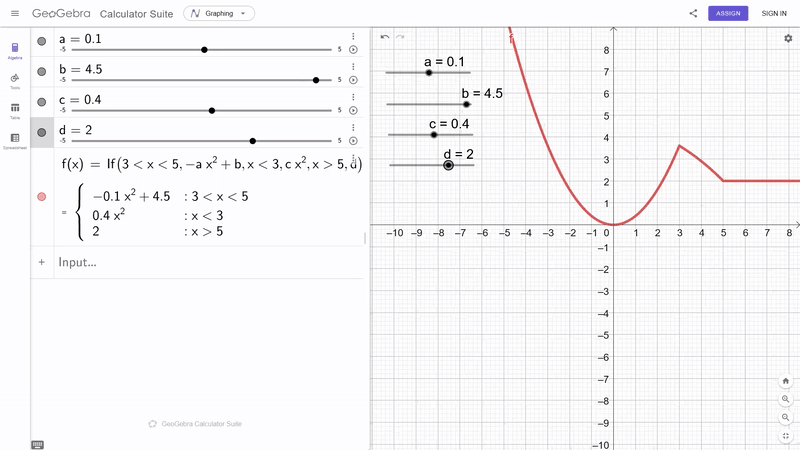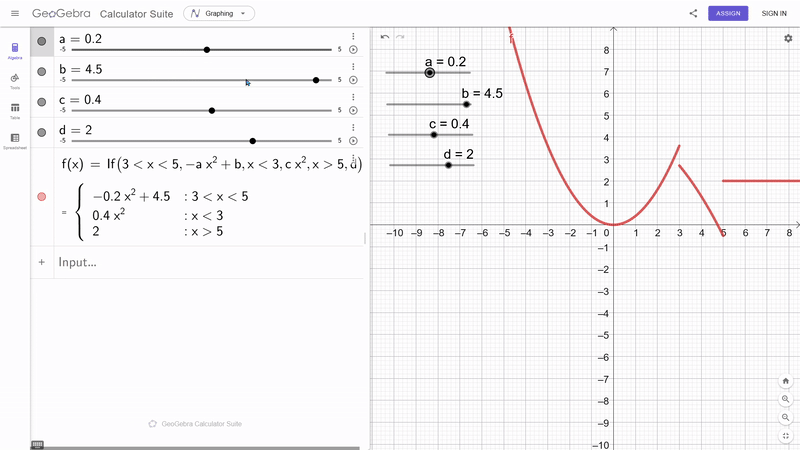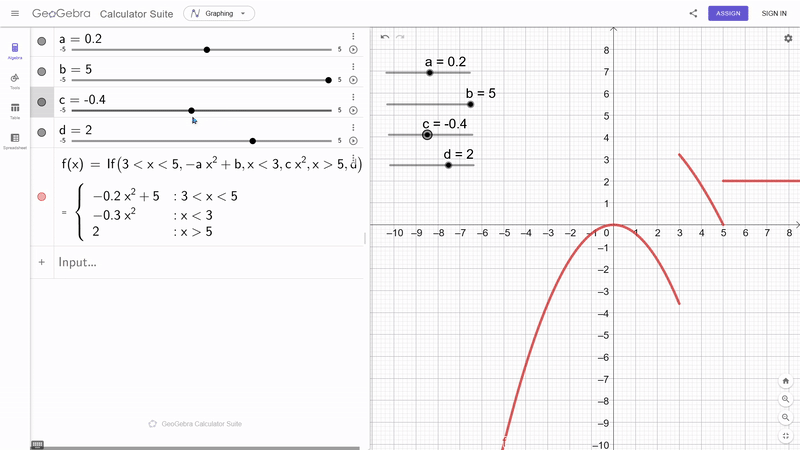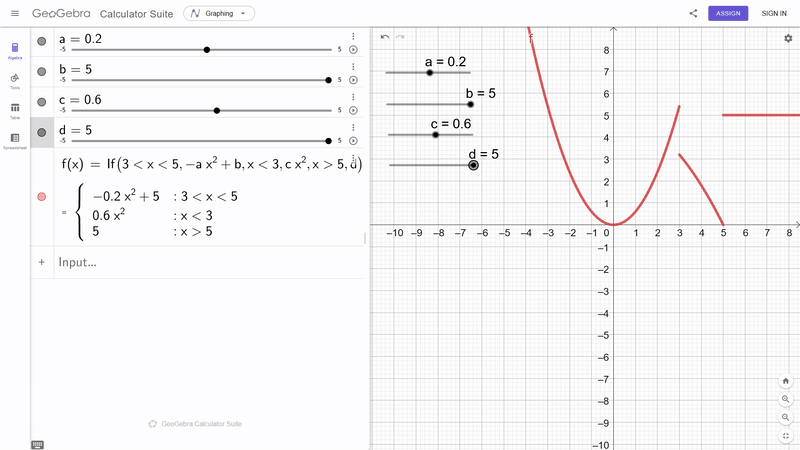
- Global:
Beispiele aus der Praxis
| Kurve | global | st├╝ckweise |
|---|---|---|
| polynomial | Bezier | B-Spline |
| rational | rat. Bezier | NURBS |
NURBS = Non-uniform Rational B-Splines
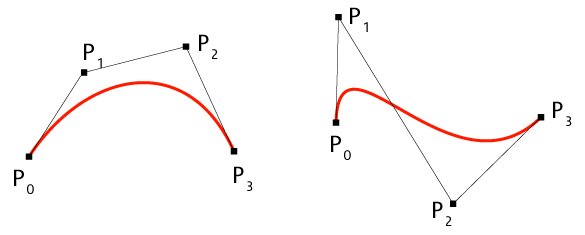
Beispiel kubischer Bezierkurven:
