Computergrafik
Spekulare Reflektion (Phong Modell)
← Diffuse Reflektion | ● | Materialfarben →
Reflektion an einer nicht ideal spiegelnden Oberfläche:
Licht wird nur unter einem Ausfallswinkel beobachtet, welcher gleich dem Einfallswinkel ist (Nicht-uniforme BRDF).
Einfallswinkel = Ausfallswinkel
Flächen sind nicht ideal spiegelnd, d.h. Glanzlicht in einem schmalen Winkelbereich um den Ausfallswinkel.
Phong Exponent $n$ simuliert das Glanzlicht um den Ausfallswinkel, R reflektierter Lichtvektor, V Betrachterrichtung (R, V jeweils normalisiert!):
$I = (R\cdot V)^n I_{L_s}$
Je höher der Exponent, desto schmaler der Winkelbereich des Glanzlichts. Idealer Spiegel: $n\rightarrow\infty$. Ambientes Licht: $n=0$.
$ I_{specular} = \sum_{l\in L} k_s max(R\cdot V, 0)^n I_{L_s} $
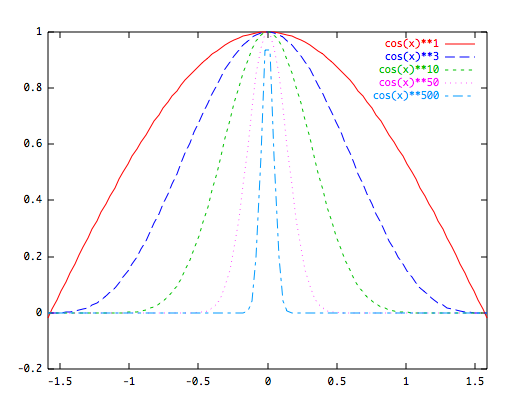
- $k_s$ ist die spekulare Materialfarbe
- Reflektionsvektor $R = 2(L\cdot N)N - L$
Alternativ über Halfway-Vektor (Blinn-Phong):
$ H = \frac{L+V}{|L+V|} $
$ cos^{-1} R\cdot V = 2 cos^{-1} H\cdot N $
- Der Winkel zwischen H und N ist halb so groß wie der zwischen R und V
- Dieser Faktor kann ignoriert werden, da die Berechnung sowieso eine Approximation darstellt
- Kann näherungsweise durch Halbierung des Exponenten kompensiert werden
- Normierung von H aufwändiger als Skalarprodukt von R und V
- aber keine Berechnung des Reflektionsvektors nötig
also: $ I_{specular} = \sum_{l\in L} k_s max(H\cdot N, 0)^n I_{L_s} $
← Diffuse Reflektion | ● | Materialfarben →